Can Topology Prevent Another Financial Crash?
 |
Stock exchange crisis (Can Topology Prevent Another Financial Crash?) |
नए नियम वैश्विक वित्त के पुनर्गठन के लिए नेटवर्क विज्ञान को लागू कर रहे हैं
क्या केविन बेकन हमें 2008 के वित्तीय संकट से बचा सकते थे? शायद ऩही। लेकिन केविन बेकन के छह डिग्री के पीछे नेटवर्क विज्ञान बस अच्छी तरह से हो सकता है।
प्रसिद्ध कहावत के अनुसार, हर फिल्म अभिनेता केविन बेकन से छह डिग्री अलग या उससे कम, सह-कलाकार से सह-कलाकार तक जा रहा होता है (वास्तव में बेकन केवल तीन डिग्री से अलग हो जाते हैं)। अभिनेता एक "छोटे-विश्व" नेटवर्क का निर्माण करते हैं, जिसका अर्थ है कि किसी एक सदस्य से किसी अन्य व्यक्ति को प्राप्त करने के लिए आश्चर्यजनक रूप से कम संख्या में कनेक्शन होते हैं। सभी प्रकार के प्राकृतिक और मानव निर्मित छोटे-विश्व नेटवर्क बेहद सामान्य हैं: पश्चिमी संयुक्त राज्य अमेरिका की इलेक्ट्रिक पावर ग्रिड, नेमाटोड वर्म सी। एलिगेंस का तंत्रिका नेटवर्क, जीव विज्ञान में इंटरनेट, प्रोटीन और जीन नेटवर्क, वैज्ञानिक में उद्धरण कागजात, और अधिकांश सामाजिक नेटवर्क छोटे हैं।
 |
Can Topology Prevent Another Financial Crash? |
इनमें से अधिकांश छोटे नेटवर्क अन्य नोड्स के लिए विशेष रूप से बड़ी संख्या में लिंक के साथ हब, या नोड का उपयोग करते हैं। केविन बेकन एक केंद्र है, क्योंकि उसने कई फिल्मों में अभिनय किया है। सी। एलिगेंस के छोटे मस्तिष्क में आरएमजी न्यूरॉन भी एक केंद्र है और अपने सामाजिक व्यवहारों (जैसे वे हैं) का समन्वय करता है। हब अन्यथा दूर के नोड्स के बीच शॉर्टकट की आपूर्ति करके छोटे-छोटे संसार बनाते हैं। और यह एक बहुत अच्छी बात हो सकती है।
1978 के बाद एयरलाइन एयरलाइन अधिनियम ने सरकारी नियंत्रण को समाप्त कर दिया, उदाहरण के लिए, एयरलाइनों ने हब-एंड-प्रवक्ता उड़ान मार्ग को स्थानांतरित कर दिया। एयरफेयर नीचे चला गया और कब्जे वाली सीटें कुल के 50 से 85 प्रतिशत तक बढ़ गईं। जब 90 के दशक में लोवे के हार्डवेयर स्टोर एक हब-एंड-स्पोक डिस्ट्रीब्यूशन सिस्टम में बदल गए, तो हर 30 या उसके स्टोर को सेवा देने के लिए एक 30-फुटबॉल-फील्ड-बड़ा केंद्र बनाकर - इसने वितरण लागत में 40 से 50 के बीच कटौती की प्रतिशत।
जब तक आप वित्त के बारे में नहीं जानते हैं, मैं शर्त लगाता हूं कि आपने एक ही वाक्य में "टोपोलॉजी" और "2008 के वित्तीय संकट" शब्द नहीं सुना होगा।
यह दक्षता छोटे नेटवर्क के जटिल संचालन को समेकित करने के तरीके से आती है। लिंक बनाना और बनाए रखना महंगा हो सकता है, और छोटे नेटवर्क उनमें से कम हैं। हब्स और प्रवक्ता पर आधारित नेटवर्क भी सरल और यादृच्छिक नोड विफलताओं के खिलाफ मजबूत हैं - क्योंकि अधिकांश नोड नोटहब हैं और इसलिए नेटवर्क के संचालन के लिए बहुत महत्वपूर्ण नहीं हैं।
जो हमें केविन बेकन और 2008 में वापस लाता है। आपको लगता है कि, यदि आप वास्तव में एक महत्वपूर्ण नेटवर्क डिजाइन कर रहे थे, जैसे, वैश्विक वित्तीय प्रणाली, आप एक छोटे से विश्व नेटवर्क का उपयोग करना चाहते हैं, बहुत कम के साथ हब्स की संख्या। हालांकि, यह नहीं है कि हमारे वित्तीय नेटवर्क क्या दिखते थे - हाल ही में।
 |
Can Topology Prevent Another Financial Crash? |
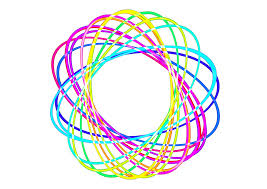
दुनिया का सबसे बड़ा बाजार: क्रेडिट डिफ़ॉल्ट स्वैप बाजार का एक नक्शा। प्रत्येक डॉट एक बैंक या अन्य वित्तीय संस्थान का प्रतिनिधित्व करता है (हम सिर्फ उन्हें बैंक कहते हैं)। ब्लू डॉट्स क्रेडिट डिफॉल्ट स्वैप के शुद्ध खरीदार हैं, लाल वाले विक्रेता हैं। लाइनें दर्शाती हैं कि किन बैंकों ने एक-दूसरे के साथ कारोबार किया है। बैंक ऑफ इंटरनेशनल सेटलमेंट्स के हालिया अनुमान के अनुसार, वैश्विक रूप से ओटीसी व्युत्पन्न अनुबंधों का कुल मूल्य $ 493 ट्रिलियन है। संदर्भ के लिए, विश्व बैंक के अनुसार 2015 में वैश्विक सकल घरेलू उत्पाद $ 77.9 ट्रिलियन था।
गन्दी दिखने वाली आकृति ने क्रेडिट डिफ़ॉल्ट स्वैप (सीडीएस) बाजार नेटवर्क का प्रतिनिधित्व किया, और बहुत छोटे डोरियों में बहुत अधिक डोरियों की तरह देखा। जिस तरह से बैंकों ने परंपरागत रूप से कारोबार किया है, उससे उलट नतीजे आए हैं, जिन्हें ओटीसी के लिए "ओवर-द-काउंटर" कहा जाता है: सीधे, स्वतंत्र रूप से, जब भी, और हालांकि वे चाहें। यह 1970 के दशक के बाद से सबसे अधिक डेरिवेटिव खरीदा और बेचा गया है, जब डेरिवेटिव में उछाल ने उन्हें दुनिया का सबसे बड़ा बाजार बना दिया। आज, दुनिया के सभी शेयर और बॉन्ड बाजारों की तुलना में डेरिवेटिव ट्रेडिंग से वित्तीय प्रणाली के माध्यम से अधिक पैसा बहता है।
येलन ने यार्न की टंगल्स की अपनी गेंद के साथ समस्या ली। यदि CDS नेटवर्क को हब-एंड-स्पोक आकार में पुन: कॉन्फ़िगर किया गया था, तो येलन ने कहा, यह अधिक सुरक्षित होगा - और यह वास्तव में, संकट के बाद के वित्तीय विनियमन का एक जोर है। केविन बेकन और लोव्स हार्डवेयर की दक्षता और सरलता वैश्विक व्युत्पन्न व्यापार पर लागू की जा रही है।
SANITIZED: क्रेडिट डिफॉल्ट स्वैप मार्केट का एकल-हब और स्पोकन संस्करण। चार्ट: जेनेट एल येलन
सितंबर 2009 में संकट के मद्देनजर, G20 (विकसित राष्ट्रों की मुख्य आर्थिक परिषद) के नेताओं ने पिट्सबर्ग में मुलाकात की और हब-एंड-स्पोक नेटवर्क को लागू करने के लिए काम किया। वे "स्पष्ट जनादेश" नामक कुछ लगाने के लिए सहमत हुए। ओटीसी व्युत्पन्न बाजार पर - एक विनियमन का अर्थ है कि वित्तीय प्रणाली को हब और प्रवक्ता को अनिवार्य बनाकर सुरक्षित करना। शासनादेश आवश्यक है कि सभी मानक ओटीसी डेरिवेटिव एक्सचेंजों पर कारोबार किया जाए और केंद्रीय समाशोधन समकक्षों, या एसीपी के माध्यम से मंजूरी दे दी जाए। CCPs बस कंपनियां हैं जो डेरिवेटिव्स के खरीदारों और विक्रेताओं के बीच खड़ी होती हैं। 2010 में, डोड-फ्रैंक कानून ने यू.एस. में इस आवश्यकता को संहिताबद्ध किया। अन्य देशों ने तब से सूट किया है। अब, फ्री-फॉर-दैट के विपरीत जो पहले व्युत्पन्न व्यापार पर हावी था, ज्यादातर समय, जब बैंक ए बैंक बी से व्युत्पन्न एक्स खरीदना चाहता है, बी को पहले एक्स को एक सीसीपी को बेचना चाहिए, जो तब घूमता है और एक्स बेचता है को ए।
और वह आवश्यकता येलन की पहली तस्वीर में सीडीएस नेटवर्क को ले जाती है, और इसे हब के सीसीपी के साथ इसे सुव्यवस्थित हब के रूप में पेश करती है और अपने दूसरे की बात करती है।
जनादेश का कार्यान्वयन अभी भी एक कार्य प्रगति पर है, लेकिन ज्यादातर यह एक सौदा है। ब्याज दर व्युत्पन्न में ओटीसी बाजार का लगभग 80 प्रतिशत शामिल है और अब, जनादेश के कारण, यूएस में सीएमई क्लीयरिंग और यूरोप में एलसीएच क्लैरेट के स्वैक्लियर जैसे सीसीपी प्रत्येक सप्ताह ब्याज दर के 70 प्रतिशत को मंजूरी दे रहे हैं। क्रेडिट क्रेडिट भी हैं साथ में, 79 प्रतिशत पर। येलेन इस प्रगति को सिस्टम को सुरक्षित बनाने की दिशा में विचार करता है।
यह विचार कि वित्तीय संलयन और प्रणालीगत जोखिम के लिए एक वित्तीय नेटवर्क के आकार (या टोपोलॉजी) का महत्वपूर्ण योगदान हो सकता है, और अपेक्षाकृत स्पष्ट नहीं है। वास्तव में, जब तक आप वित्त का एक अंश नहीं रखते हैं, तो मैं शर्त लगाता हूं कि आपने "टोपोलॉजी" और "2008 के वित्तीय संकट" शब्दों को एक ही वाक्य में नहीं सुना होगा।
टोपोलॉजी को 2008 के गणितीय संदर्भ के रूप में समझें। जिस तरह खतरनाक ऋण देने के तरीके हैं, उसी तरह खतरनाक टोपोलॉजी भी हैं। यह एक, उदाहरण के लिए:
ट्रोलिंग के लिए प्रतीक्षा: इस खिलौना नेटवर्क में, प्रत्येक बॉक्स एक बैंक का प्रतिनिधित्व करता है। बैंकों के बीच के तीर ऋण का प्रतिनिधित्व करते हैं: बैंक ए का बैंक बी पैसा है; B, C पर समान राशि बकाया है, और इसी तरह। चित्रण: एलन, एफ। एंड गेल, डी। वित्तीय छूत। राजनीतिक अर्थव्यवस्था की पत्रिका 108, 1-33 (2000)।
इस नेटवर्क में चार बैंक (और उनके द्वारा बकाया राशि) समान हैं: प्रत्येक में पूंजी की समान राशि है, जिसका अर्थ है कि दिवालिया होने से पहले नुकसान की समान क्षमता। आप एक बैंक के ईंधन के रूप में पूंजी के बारे में सोच सकते हैं: अपने गियर को बंद करने के लिए पीसने से पहले अपने टैंक से ली जाने वाली राशि।
अब, कल्पना कीजिए कि बैंक ए पैसे का एक गुच्छा खो देता है, पर्याप्त है कि यह दिवालिया हो जाता है और यह बी को भुगतान करने वाले सभी का भुगतान नहीं करता है। उस स्थिति में, बी को एक नुकसान भी होता है। और अगर बी का नुकसान इसकी पूंजी से अधिक है, तो यह भी नीचे चला जाएगा। यदि A और B मिलकर पर्याप्त हार जाते हैं, तो C भी विफल हो जाएगा। अंत में, एक नुकसान, या रिसाव, सभी पूंजी की कुल राशि को निकालने के लिए पर्याप्त है कि नेटवर्क के सभी बैंकों ने पूरी प्रणाली को नीचे ले जाएगा।
अब इसके विपरीत जो निम्न नेटवर्क में होता है:
4.इंटरकनेक्टेड:
इस मॉडल में, बैंकों के बीच अधिक से अधिक कनेक्शन नेटवर्क को अधिक से अधिक आघात को अवशोषित करने की अनुमति देता है। चित्रण: एलन, एफ। एंड गेल, डी। वित्तीय छूत। राजनीतिक अर्थव्यवस्था की पत्रिका 108, 1-33 (2000)।
बैंक स्वयं पहले जैसे ही हैं: उन सभी के पास एक ही पूंजी और एक ही ऋण है। केवल एक चीज है जो नेटवर्क की टोपोलॉजी है: कौन किससे और कितना उधार ले रहा है। इस बार सभी बैंकों ने अपने उधार और ऋण को चारों ओर फैला दिया है, जिससे नेटवर्क अधिक जुड़ा हुआ है। उदाहरण के लिए, बैंक ए के पास पहले की तरह ही ऋण है, लेकिन इस बार इसका एक तिहाई बी, सी, डी और डी पर बकाया है।
तो फिर से कल्पना करें कि स्प्रिंग्स एक रिसाव है, ताकि एक निश्चित मात्रा में राजकोषीय द्रव प्रणाली से बाहर निकल जाए। इस बार अंतर यह है कि ए की कमी (यह जो बकाया है और जो भुगतान कर सकता है, उसके बीच का अंतर) बैंकों बी, सी और डी के बीच समान रूप से विभाजित है, इसलिए बी, सी और डी में से प्रत्येक नुकसान का सिर्फ एक तिहाई हिस्सा है। B ने पहले किया था। और इसका मतलब है कि A को दूसरे बैंक को लेने के लिए पहले की तुलना में तीन गुना बड़ा घाटा होना चाहिए। यह दूसरे नेटवर्क का अधिक जुड़ा हुआ टोपोलॉजी इसके रिंग-आकार वाले रिश्तेदार की तुलना में एक बड़े झटके को अवशोषित करने में सक्षम बनाता है।
2008 में एक बड़ा कारण क्रेडिट बाजार जम गया था, बस भ्रम था कि कौन किसके सामने आया।
ये चार-बैंक नेटवर्क उदाहरण 2000 में अर्थशास्त्रियों फ्रेंकलिन एलेन और डगलस गेल द्वारा लिखे गए एक प्रभावशाली पत्र से आए हैं। उनका मॉडल और विश्लेषण जितना मैंने यहां वर्णित किया है, उससे कहीं अधिक परिष्कृत था, लेकिन वे एक ही निष्कर्ष पर आते हैं: अधिक जुड़ा हुआ एक वित्तीय नेटवर्क है, और अधिक मजबूत है, जिसका अर्थ है कि बैंक विफलताओं के अनुक्रम को ट्रिगर करने के लिए एक बड़ा झटका लगता है।
दूसरी ओर, यह छोटा सा चार-बैंक मॉडल अत्यधिक जुड़े नेटवर्क की एक खतरनाक विशेषता को भी दिखाता है। जैसा कि एलन और गेल ने अपने पेपर में बताया, सभी चार बैंकों की पूंजी को खत्म करने के लिए पर्याप्त नुकसान एक पूरी तरह से जुड़े नेटवर्क को नीचे लाएगा, निश्चित रूप से यह रिंग के आकार का एक नीचे लाएगा। अंतर यह है कि, जबकि रिंग नेटवर्क एक समय में एक बैंक में विफल रहता है, पूरी तरह से जुड़ा हुआ एक अचानक और सभी एक बार में विफल रहता है। यह बैंक ऑफ इंग्लैंड के मुख्य अर्थशास्त्री और कार्यकारी निदेशक, एंड्रयू हैल्डेन, अत्यधिक जुड़े नेटवर्क की "मजबूत अभी तक नाजुक" गुणधर्म कहते हैं
वास्तव में, हाल्डेन कहते हैं, वास्तविक वित्तीय नेटवर्क की अत्यधिक जुड़ी हुई प्रकृति ने पिछले संकट के "बीज बोए थे"। लेकिन हम कैसे जानते हैं कि हल्दाने और येलन दोनों का समर्थन करने वाले हब-एंड-स्पोक समाधान अनजाने परिणामों की कीमत पर एक प्रकार के खतरे को कम नहीं करते हैं जो और भी खतरनाक हो सकते हैं?
यह अर्थशास्त्र का सवाल है, ऐसा विशेषज्ञों को खोजना मुश्किल नहीं है जो सोचते हैं कि वास्तव में ऐसा ही है।
मुझे ब्लूमबर्ग टीवी पर लाइव देखने के कुछ मिनट बाद फोन पर यूनिवर्सिटी ऑफ ह्यूस्टन के फाइनेंस प्रोफेसर क्रेग पियरसॉन्ग को मिल गया, जहां उन्होंने पूछा कि क्या "नहीं" कहा गया है कि क्या सीसीपी सिस्टम को अधिक ध्वनि बना रहे हैं।
उन्होंने कहा, "यह सही है, हाँ," जब मैंने उन्हें याद दिलाया। "कभी-कभी मुझे ऐसा लगता है कि मुझे कैंपफ़ायर के बगल में अपनी ठोड़ी के नीचे टॉर्च के साथ बात करनी चाहिए।"
CCPs को जोखिम जोखिम को कम करने के लिए माना जाता है जोखिम लेनदारों की कुल राशि को व्युत्पन्न व्यापार से देनदारों को कम करना है। उदाहरण के लिए, उदाहरण के लिए, डेरिवेटिव के कारण, रिंग बैंक के आकार वाले चार-बैंक नेटवर्क में प्रत्येक बैंक ने अगले 100 मिलियन का बकाया देखा। तब सिस्टम में कुल क्रेडिट एक्सपोज़र $ 400 मिलियन होगा, क्योंकि लेनदारों के पास कुल राशि का जोखिम है। दूसरी ओर, यदि सभी बैंक एक-दूसरे के साथ CCP के माध्यम से कारोबार करते हैं, तो, चूंकि प्रत्येक बैंक CCP $ 100 मिलियन का बकाया होगा और CCP $ 100 मिलियन का बकाया होगा, इसलिए दोनों ऋण रद्द कर दिए जाएंगे और शून्य पर शुद्ध हो जाएंगे। प्रणाली में भव्य कुल ऋण जोखिम भी शून्य होगा।
अधिक यथार्थवादी परिदृश्यों में, एक CCP ने सिस्टम के क्रेडिट एक्सपोज़र को शून्य से कम नहीं किया, लेकिन जो हब और स्पोक आकार बनाता है, वह अभी भी इसे कम करेगा। यह नेटवर्क में कम लिंक के माध्यम से सिस्टम के ऋणों को फ़नलिंग करके, नेटिंग के लिए अधिक अवसर प्रदान करता है। यह एयरलाइन मामले के समान है जहां हब-एंड-स्पोक रूटिंग मार्गों की संख्या कम कर देता है, जिससे यात्रियों को उड़ानों को साझा करने का अधिक अवसर मिलता है। उस स्थिति में, लाभ कम खाली सीटें हैं। वित्तीय मामले में, लाभ कम क्रेडिट जोखिम है। उस एक्सपोजर का हाल ही में बैंक ऑफ इंटरनेशनल सेटलमेंट्स ने अनुमान लगाया था कि वह $ 2008 ट्रिलियन से घटकर 2.9 ट्रिलियन डॉलर रह जाएगा, जो कि 2008 के अंत में CCPs के कारण हुआ था।
"हम अभी भी वित्तीय नेटवर्क के मानचित्रण के पत्थर की उम्र में थोड़ा सा हैं। यह वास्तव में भयावह हिस्सा है।
हब-एंड-स्पोक्स का सरल आकार - उनके कनेक्शन और मार्गों की छोटी संख्या, उनके आसानी से समझ में आने वाले प्रवाह - पारदर्शिता को भी बढ़ावा देते हैं, जो स्वयं जोखिम को कम करता है। 2008 में एक बड़ा कारण क्रेडिट बाजार जम गया था, बस भ्रम था कि कौन किसके सामने आया। जैसा कि स्टैनफोर्ड के वित्त और व्युत्पन्न विशेषज्ञ डेरेल डफी ने कहा, लेहमैन के निधन के लिए बैंकरों की मानसिकता की नकल करते हुए, "गोश, अगर लेहमैन विफल रहा, तो लेहमैन से जुड़े अन्य कौन विफल हो सकते हैं?" और जो मैं उससे जुड़ा हूं वह लेहमैन से जुड़ा हो सकता है जो विफल हो सकता है? गोश, यह वास्तव में जटिल है। मुझे लगता है कि मैं केवल क्रेडिट प्रदान करना बंद करने जा रहा हूं।
शिपर्स, रिटेलर्स और एयरलाइंस को समान कारणों से हब और स्पोक्स से फायदा होता है। एयरलाइंस के पास ट्रैक रखने के लिए कम मार्ग हैं। फास्ट-फूड चेन में साल्मोनेला और अन्य दूषित पदार्थों के स्रोत को ट्रैक करने का एक आसान समय है।
वास्तव में, डफी ने कहा कि नियामकों और नेताओं के उत्साह के बारे में स्पष्ट जनादेश के लिए, “यह इतना अधिक नहीं था कि लोगों को भरोसा था कि यह जोखिम को कम करने वाला था। यह मूल रूप से अधिक पारदर्शिता बनाने का एक तरीका था, और उस प्रकार के जोखिम के बारे में अधिक आश्वस्त होना जो हम वास्तव में सामना करते हैं। ”
बड़े बैंकों ने लंबे समय तक वित्तीय नेटवर्क में हब के रूप में कार्य किया है, जिससे यह छोटा हो गया है। CCPs के साथ अंतर यह है कि बड़े बैंकों की तुलना में उनमें से बहुत कम हैं, जिससे वे एक छोटी सी दुनिया को भी छोटा बना रहे हैं। इसके अलावा, CCPs में एक और केवल एक ही काम करने का गुण है: दोनों पक्षों के बीच का व्यापार। वे बैंकों की तुलना में बहुत सरल और अधिक पारदर्शी हैं, और जैसा कि डफी बताते हैं, “CCP अर्जेंटीना को, या एरिज़ोना में रियल एस्टेट विकास के लिए पैसा उधार नहीं दे सकता है, जबकि बैंक कर सकते हैं। इसमें जोखिम लेने का कोई विवेक नहीं है। "
 |
Can Topology Prevent Another Financial Crash? |
5.FORECLOSED:
2008 का संकट, जिसने पूरे संयुक्त राज्य अमेरिका में फौजदारी की लहर फैला दी थी, डेरिवेटिव बाजारों के पेचीदा टोपोलॉजी द्वारा भाग में लाया गया था।
और फिर भी, ऐसे लोग हैं जो आश्वस्त नहीं हैं।
जब मैंने तर्क दिया कि CCPs फ्रेंकलिन एलेन के सामने जोखिम भरे व्यवहार में शामिल नहीं होंगे, जो डफी की तुलना में सुरक्षा में उनके योगदान पर अधिक संदेह करते हैं, तो उन्होंने पीछे धकेल दिया। "मैं इससे असहमत हूं," उन्होंने कहा, "क्योंकि यदि आप निक लेसन और बारिंग्स जैसे इन डेरिवेटिव घोटालों को देखते हैं, तो इन जोखिमों को नियंत्रित करना बहुत मुश्किल है, इसलिए जब धोखाधड़ी और चीजें शामिल होती हैं, तो यह सिर्फ इतना है कि चीजें डॉन ' t काम बहुत अच्छा है। तब आपको इन भयावह विफलताओं के लिए क्षमता मिलती है। ”
पीरॉन्ग का नज़रिया यह है कि नियामक इसे कम करने के बजाय केवल जोखिम उठा रहे हैं। "आप मूल रूप से गुब्बारे को एक सिरे से निचोड़ते हैं और यह सिर्फ दूसरे को बाहर निकालता है," उसने मुझे बताया, सारांश यह है कि वह क्लियरिंग जनादेश को सबसे अधिक व्यापार-बंद के रूप में मानता है: कुल क्रेडिट जोखिम (जिसे सीसीपी को कम करना चाहिए) के बीच और "तरलता जोखिम" जो CCPs वास्तव में बढ़ सकता है।
वित्त में तरलता का अर्थ है नकदी तक पहुंच, या नकदी के लिए आसानी से बेची गई संपत्ति। तरलता जोखिम की आवश्यकता होने पर तरलता नहीं होने का खतरा होता है। CCPs संकट के दौरान एक तरलता की कमी को बढ़ा सकते हैं क्योंकि वे बैंक की चूक से खुद को बचाते हैं:बैंकों को CCP में न केवल उन ऋणों के खिलाफ जमानत देने के लिए कठोर नियमों को लागू करने की आवश्यकता होती है, लेकिन उन ऋणों के विरुद्ध जो बैंक संभवतः CCP को दे सकते हैं। CCPs संपार्श्विक के रूप में तरल संपत्ति की मांग करते हैं। इसलिए, उच्च बाजार में उतार-चढ़ाव या दुर्घटना के कारण CCPs को अपने आप को बचाने के लिए बैंकों पर बड़े मार्जिन से कॉल करने की जरूरत पड़ सकती है, जब यह सबसे ज्यादा जरूरत होती है। और इससे कुछ बैंक अपने अन्य अल्पकालिक ऋणों पर चूक कर सकते हैं, जिससे उन्हें सीसीपी के लिए अनिवार्य रूप से दिवालिया हो जाना पड़ता है।
पीरॉन्ग को इस बात की भी चिंता है कि क्लीयरिंग जनादेश का असर वित्तीय नेटवर्क के सदस्यों पर पड़ेगा, जो ट्रेड डेरिवेटिव बिल्कुल नहीं करते हैं। उनके एक कागजात से पता चलता है कि कैसे CCPs की नेटिंग और मार्जिनिंग की आवश्यकताएं बैंकों को अन्य लेनदारों को कम कर सकती हैं - जैसे कि मुद्रा बाजार फंड, जो कि डेरिवेटिव के बजाय ऋण के माध्यम से बैंकों को उधार देते हैं - यदि बैंक दिवालिया हो जाता है तो पुनर्प्राप्त करें।
"एक प्रणालीगत दृष्टिकोण से," पीरॉन्ग ने कहा, "हर किसी को देखकर, यह स्पष्ट नहीं है कि एक्सपोज़र कम हो गए हैं। कुछ एक्सपोज़र कम कर दिए गए हैं, लेकिन अन्य एक्सपोज़र बढ़ा दिए गए हैं। ”
सहयोगी हॉक्सियांग झू के साथ डफी ने दिखाया है कि सीसीपी हमेशा कुल ऋण जोखिम को कम नहीं करते हैं, और वास्तव में इसे बढ़ा सकते हैं। ऐसा इसलिए हो सकता है क्योंकि बैंकों के बीच फायदेमंद नेटिंग तब भी होती है जब वे सीधे एक-दूसरे के साथ व्यापार करते हैं - उनके व्यापार आम तौर पर ऋण में परिणाम दोनों तरीके से निर्देशित किया। वास्तविक-विश्व CCPs आमतौर पर उन सभी ट्रेडों के बीच खड़े नहीं होते हैं जो दो समकक्षों ने एक-दूसरे के साथ किए हैं, लेकिन केवल कुछ। इसलिए, एक सीसीपी के शुद्ध लाभ नेटिंग लाभ की कीमत पर आते हैं जो द्विपक्षीय प्रणाली अन्यथा होती थी।
डफी ने पारंपरिक ज्ञान के बारे में मुझसे कहा, "मुझे नहीं लगता कि किसी ने वास्तव में सीसीपी के बाहर बहुपक्षीय जाल के बीच इस व्यापार-बंद पर विचार किया था।" जबकि उनका मानना है कि नियामक स्पष्ट समाशोधन को अपनाने के लिए सही थे, उनका यह भी मानना है कि "उनकी नियोजन प्रक्रियाएं शायद इतनी अच्छी नहीं थीं, कि उनके पास यह विश्वास करने के लिए विश्लेषण नहीं था कि यह वास्तव में जोखिम का एक महत्वपूर्ण कमी होगा। शुरू होने से पहले। ”
यह अभी भी समस्या का हिस्सा है, जो एक समस्या को देखते हैं: कि वित्तीय नेटवर्क इतना बड़ा और जटिल है कि केवल व्यापक डेटा और इसके पूर्ण मॉडलिंग से हमें यह बताने की उम्मीद है कि क्या जनादेश, अन्य व्युत्पन्न का उल्लेख नहीं करना है नियम, वास्तव में अच्छा कर रहे हैं।इस विषय पर हाल के अर्थशास्त्र साहित्य की एक स्कैन से पता चलता है कि इसमें से अधिकांश खिलौना मॉडल पर ध्यान केंद्रित करते हैं, जैसे कि एलन और गेल, वास्तविक दुनिया के नाटकीय सरलीकरण हैं। यह एक आवश्यक पहला कदम है, क्योंकि आपको चलने से पहले चलना चाहिए, और क्योंकि पूर्ण वित्तीय नेटवर्क को चिह्नित करने के लिए डेटा अभी तक उपलब्ध नहीं है।
लेकिन अभी के लिए, स्टैनफोर्ड में डफी के सहयोगी के रूप में, अर्थशास्त्री मैथ्यू जैक्सन ने मुझसे कहा, "हम अभी भी वित्तीय नेटवर्क के मानचित्रण के पत्थर की उम्र में थोड़ा सा हैं। बहुत सारे लोग महसूस करते हैं कि यह एक मुद्दा है और हम अभी तक उपकरण के साथ सुसज्जित नहीं हैं कि वास्तव में एक अच्छा काम करते हैं, इसलिए हम यह कहना आश्वस्त हैं कि हमें वास्तव में यह नियंत्रण में है ... यह वास्तव में भयावह हिस्सा है। "
वास्तव में, स्थिति इससे भी अधिक पेचीदा है, क्योंकि एक बार भी सभी डेटा और मॉडल जो हम ऑनलाइन चाहते हैं, अभी भी व्यापार-बंद होंगे जो अकेले विज्ञान नहीं कर सकता है। जैक्सन ने कहा, उदाहरण के लिए, "कौन सा नेटवर्क इष्टतम है यह इस बात पर निर्भर करता है कि आप इसे किस तरह के झटके के साथ मार रहे हैं ... कुछ वास्तव में बहुत सारे छोटे बदलावों के लिए मजबूत हो सकता है और तब यह एक विनाशकारी नेटवर्क हो सकता है जब यह एक बड़े वित्तीय मंदी की ओर आता है एक बड़ी फर्म। ”
फिर एक बात यह है कि मेरे द्वारा सहमति व्यक्त की गई प्रत्येक अर्थशास्त्री कमरे में हाथी था: सीसीपी ही विफल रहता है।
हब विफलता हब-एंड-स्पोक नेटवर्क का अकिलीस एड़ी है। यही कारण है कि कार्यकर्ता अपनी रानी की रक्षा करने के लिए झुंड में रहते हैं, क्यों जीवविज्ञानी जोर्डी बासकोम्प्टे ने उच्च संरक्षण प्राथमिकताओं को प्राप्त करने के लिए परागण नेटवर्क में हब प्रजातियों का आह्वान किया है, have 9/11 के बाद से सैनिकों ने ग्रैंड सेंट्रल टर्मिनल पर गश्त क्यों की है, और नियामक द्वारा सीसीपी की आवश्यकता क्यों है संपार्श्विक इकट्ठा करने के लिए।
CCPs अतीत में विफल रहे हैं, लेकिन केवल छोटे बाजारों में। अब जब वे दुनिया के सबसे बड़े बाजार के केंद्र में हैं, एलन ने मुझसे कहा, "यह उस तरह के प्रणालीगत जोखिम के कारण संकट की संभावना को कम करता है, लेकिन अगर ऐसा संकट उत्पन्न होने वाला था, यह अधिक गंभीर होगा। "
दूसरे शब्दों में, CCPs ने बाज़ार के सभी अंडों को एक टोकरी में रख दिया।
डफी उस रूपक की तरह नहीं है ("अच्छी तरह से गणितीय रूप से अच्छी तरह से सूचित किया गया है ... नेटिंग के कारण"), और वह बताता है कि एक बड़ी नोड की विफलता जरूरी नहीं है कि कई छोटे नोड विफल होते हैं। वह जो सबसे महत्वपूर्ण है, वह कहता है, क्या नियामकों ने सीसीपी की विफलता की संभावना को "पर्याप्त रूप से छोटा" बना दिया है और दूसरा, क्या उनके पास "एक तरीका है जो एक असफल सीसीपी के इलाज के लिए उचित है।"
जोड़ने से पहले एक अशुभ क्षण की तरह महसूस करने के लिए डफी ने रोका:
"उनके पास अभी तक एक भी नहीं है।"
यह परिचित लग सकता है। बड़े बैंकों और अन्य वित्तीय कंपनियों के संबंध में यह अनिवार्य रूप से वही स्थिति है जो 2008 में हमारे पास थी। इसने भालू-स्टर्न और एआईजी के तदर्थ खैरात और लेहमन के पतन को घेरने वाली अराजकता को जन्म दिया।
तो, क्या कोई उम्मीद है कि नेटवर्क विज्ञान दुनिया को एक और वित्तीय आपदा से बचाने में मदद करेगा? संभवतः। लेकिन अगर ऐसा है, तो यह केवल मार्क ट्वेन की कोरोलरी से सहायता के साथ होगा: "अपने सभी अंडे एक टोकरी में रख दें और -" इस तरह से देखें "।













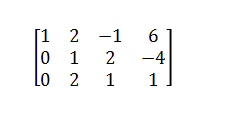
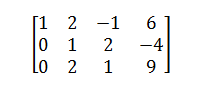






0 Comments: