Logic Theory and Basic Notation

1. संयोजकों, सप्रतिबन्ध प्रकथनों  और मात्राओं का संक्षिप्त रूप(A Brief Look At Connectives, Implications & Quantifiers)-

तर्क सिद्धांत की उत्पत्ति एक तर्क की अवधारणा से शुरू होती है। तर्क पाठ्यपुस्तकों के बहुमत में एक तर्क के लिए एक प्रारंभिक, केंद्रीय परिभाषा होती है - एक जो संभवतः निम्नलिखित की तरह लगती है:
एक तर्क में एक या अधिक विशेष वक्तव्य होते हैं, जिन्हें परिसर कहा जाता है, यह विश्वास करने के लिए एक कारण के रूप में प्रस्तुत किया जाता है कि एक और कथन, जिसे निष्कर्ष कहा जाता है, सत्य है
परिसर तर्क सिद्धांत के परमाणु हैं: सब कुछ उनसे निर्मित है। आधार एक घोषणात्मक कथन है जिसे केवल या तो सही या गलत का मूल्यांकन करना चाहिए। एक एकल आधार को एक आदिम आधार के रूप में जाना जाता है - U.S.A में 50 राज्य हैं (जो सत्य है)। कई परिसरों को एक साथ जोड़ने से एक यौगिक आधार बनता है - यूएएस में 50 राज्य हैं और आज मियामी में बर्फबारी हुई (जो कि झूठी है)। एक व्यक्ति कई कथनों को कैसे जोड़ता है? जैसा कि आप पिछले उदाहरण में देखते हैं, ऐसे ऑपरेटरों के साथ जो आप पहले से परिचित हैं, लेकिन उन्हें अपनी भाषा और वाक्यविन्यास की आवश्यकता होती है।

2.संयोजियों(Connectives)-

गणित की अन्य शाखाओं के समान, परिसर में मौलिक ऑपरेटरों का अपना सेट (जोड़ना, घटाना, आदि ...) है। तर्क सिद्धांत में, पांच बुनियादी तार्किक कनेक्टर, जिन्हें सामूहिक रूप से संयोजकों के रूप में जाना जाता है, इस भूमिका को भरते हैं। वे नीचे दी गई तालिका में संक्षेपित हैं, पी एंड क्यू अक्षर को दो आदिम परिसर का प्रतिनिधित्व करते हैं: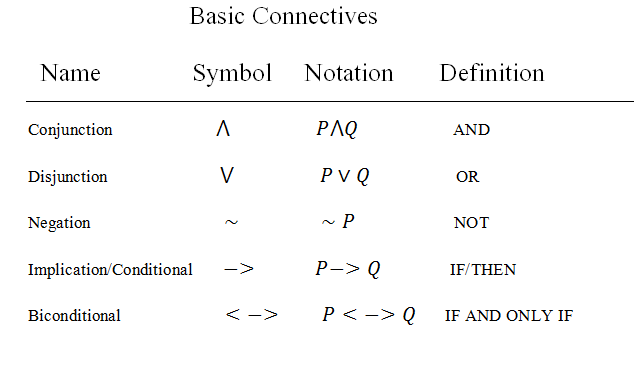

Logic Theory and Basic Notation

यदि आपको किसी भी स्तर पर प्रोग्रामिंग से अवगत कराया गया है, तो यह अत्यधिक संभावना है कि ऊपर दी गई तालिका कम से कम अस्पष्ट रूप से परिचित लगती है। इसका कारण यह है कि संयोजक आम भाषा वाक्य रचना के मूल में हैं और लगभग हमेशा कुछ विशेष वर्ण प्रत्येक संयोजी के लिए निर्दिष्ट होते हैं ((&& = और; = = या, आदि ...)।
पांच संयोजनों में से किसका उपयोग दो परिसरों के बीच एक तार्किक कनेक्टर के रूप में किया जाता है, यह परिसर के सत्य मूल्यों के आधार पर यौगिक बयान के समग्र सत्य मूल्य को निर्धारित करता है। यहां एक महत्वपूर्ण सिद्धांत जो पहली बार में सहज-ज्ञान युक्त लग सकता है, वह निकालने योग्य है: जब यौगिक कथनों का विश्लेषण किया जाए, तो यह जानना आवश्यक नहीं है कि P & Q वास्तव में क्या कहता है, केवल यह कि क्या वे भाग सही या गलत हैं।

3.सप्रतिबन्ध प्रकथन (Implication)-

पांच संयोजनों में से, एक तुरंत आगे के निरीक्षण के योग्य है - सप्रतिबन्ध प्रकथन , उर्फ, यदि-तब बयान। सप्रतिबन्ध प्रकथन  P → Q के मानक रूप के साथ एक संयोजक है जहां P को परिकल्पना (या पूर्ववृत्त) के रूप में जाना जाता है, और Q को निष्कर्ष (या परिणाम) के रूप में जाना जाता है।
जबकि सप्रतिबन्ध प्रकथन  के ऊपर एक मानक रूप है, जिसमें तीन अन्य सामान्य प्रकार के सशर्त मौजूद हैं जो समीक्षा के लायक हैं। निम्नलिखित चार सशर्तियां सरल हैं लेकिन अभी तक काफी सामान्य और शक्तिशाली यौगिक वक्तव्य हैं जो मुख्य संयोजकों के साथ सशर्त जुड़ते हैं:

Logic Theory and Basic Notation

एक सशर्त अपने आप में एक यौगिक आधार है, अर्थात, यह या तो सही या गलत का मूल्यांकन करता है। किसी भी सप्रतिबन्ध प्रकथन  के लिए, किसी भी अन्य संयोजी की तरह, यौगिक आधार का सत्य मूल्य इसके दो स्वतंत्र परिसरों के सत्य मूल्यों से निर्धारित होता है। ऊपर वर्णित परिभाषाओं के साथ, उदाहरण के लिए, एक सप्रतिबन्ध प्रकथन  या तो सच है जब परिकल्पना झूठी होती है, या जब निष्कर्ष सत्य होता है; जो झूठ बोलने के सप्रतिबन्ध प्रकथन  के लिए केवल एक ही रास्ता छोड़ता है: जब परिकल्पना सच होती है और निष्कर्ष गलत होता है।
अगर यह मानसिक रूप से ट्रैक करने के लिए बहुत कुछ लग रहा था, जैसा कि यह मेरे लिए था, तो सांस लेना आसान और आराम करें यह विश्वास दिलाता हूं कि निकट भविष्य में शक्तिशाली उपकरण हैं जो जटिल परिस्थितियों का विश्लेषण एक ब्लूप्रिंट के रूप में सरल बनाते हैं। हमारे द्वारा उपयोग किया जाने वाला मुख्य उपकरण सत्य तालिकाओं के नाम से एक निफ्टी तर्क -१०१ उपकरण है। इससे पहले कि हम सत्य सारणी में आते हैं, चलो बुनियादी तर्क सिद्धांत संकेतन के हमारे ज्ञान में एक अंतिम अंतर को भरने के लिए एक त्वरित उपाय करें। एक अजीब परिदृश्य का निरीक्षण करें - निम्नलिखित कथन एक आधार है?

x दस से बड़ा है(x is larger than ten)

4.परिमाणकों(Quantifiers)-
ओपनिंग पैराग्राफ में शुरू की गई हमारी सख्त परिभाषा के तहत, एक आधार को या तो सही या गलत का मूल्यांकन करना होगा - कथन अस्पष्ट या खुला खुला नहीं रह सकता है। जिसका अर्थ है कि चर, जैसा कि हम उन्हें बीजगणित के बाद से देख रहे थे, तर्क सिद्धांत में एक नहीं-नहीं है; कम से कम कुछ संशोधन के बिना नहीं।
ऊपर दिए गए बोल्ड स्टेटमेंट को आधार नहीं माना जाता है क्योंकि x 5 या 25 हो सकता है, जिससे कथन सही या गलत हो सकता है, लेकिन वर्तमान में ऐसा नहीं है। हालाँकि, इसका मतलब यह नहीं है कि हमें अपने उपकरण से चर को पूरी तरह से हटाना होगा। चर का उपयोग करने का एक तरीका है; प्रक्रिया को मात्रात्मक कहा जाता है, तर्क में अज्ञात चर पर सीमा को सूचित करने का एक चतुर तरीका। निम्नलिखित, अद्यतन विवरण पर एक नज़र डालें - क्या यह अब एक आधार है?

सभी एक्स के लिए, एक्स एक सौ से बड़ा है(for all x, x is larger than one hundred)-

अब जब हमने ब्रह्मांड, या डोमेन को चर के रूप में परिभाषित किया है, तो कथन अब अस्पष्ट नहीं है - यह अब एक आधार है क्योंकि यह स्पष्ट रूप से असत्य का मूल्यांकन करता है। यह "सभी एक्स के लिए" का उपयोग तर्क सिद्धांत में एक क्वांटिफायर को लागू करने के रूप में जाना जाता है। क्वांटिफायर के दो मुख्य प्रकार हैं। पहला, जिसे हमने अभी देखा है, जिसे उपयुक्त रूप से यूनिवर्सल क्वांटिफायर नाम दिया गया है। "A", एक उल्टा द्वारा तय किया गया,, यह याद रखना आसान है कि यह बयान किए गए ब्रह्मांड के भीतर सभी या हर संभव उदाहरण के लिए खड़ा है। इस दूसरे परिवर्तन का निरीक्षण करें:

एक सौ से बड़ा एक एक्स मौजूद है(there exists an x larger than one hundred)

एक बार फिर से चरों को हटाए बिना, हमने एक क्वांटिफायर लगाकर एक कथन को एक आधार में बदलने का एक तरीका खोज लिया है क्योंकि कथन अब कड़ाई से सत्य का मूल्यांकन करता है। इस दूसरे प्रकार के क्वांटिफायर को अस्तित्वमान क्वांटिफायर के रूप में जाना जाता है। एक बैकवर्ड "E", जो आमतौर पर "वहां मौजूद है" या "वहाँ है" के रूप में पढ़ता है। दोनों क्वांटिफायर को नीचे संक्षेप में प्रस्तुत किया गया है:

Logic Theory and Basic Notation

सत्य टेबल्स पर(On To Truth Tables)

अब बेसिक नोटेशन के साथ, यह सच तालिकाओं के माध्यम से प्राथमिक रूप से आवेदन करने का समय है। अगले भाग में, हम पहले तर्क में तुल्यता को परिभाषित करके शुरू करेंगे; सत्य तालिकाओं का उपयोग करने के लिए, जिसका विश्लेषण करने के लिए, यदि कोई हो, चार सशर्त हम एक दूसरे के बराबर हैं। कुछ उदाहरण कथनों का निरीक्षण करने के बाद, हम आखिरकार तर्क सिद्धांत के मूल में आ जाएंगे: प्रमाण।