A Modest Research Proposal for Mathematics Education

1,गणित शिक्षा के लिए एक मामूली शोध प्रस्ताव(A Modest Research Proposal for Mathematics Education)-

कई हजारों, या शायद लाखों, शब्दों को लिखा गया है, या तो "शिक्षा के लिए मूल बातें" दृष्टिकोण के पक्ष में, या अधिक "रचनावादी" दृष्टिकोण के पक्ष में। यह बहस राजनीतिक, और कई बार शातिर है, लेकिन यह एक आवश्यक है। यह बहस पिछले पाठयक्रम दृष्टिकोण (क्या काम किया है? क्या काम नहीं किया है?), और भविष्य में आगे बढ़ने के साथ उन्हें ताज़ा रखने की आवश्यकता के बीच निरंतर धक्का और खींचता है।
गणित के शिक्षकों के लिए, यह बहस कभी खत्म नहीं होती है। इसके सबसे अधिक पुनरावर्ती में, हमारे पास निरंतर मीडिया चक्र है जो गणित के शिक्षण और परीक्षण के स्कोर को सीखना कम कर देता है, और अक्सर एक अतीत के लिए तरस जाता है जिसमें छात्र समय सारणी और संख्या तथ्यों के साथ अधिक कुशल थे। रिड्यूसिव लॉजिकेटिव कदम "दूसरे पक्ष" को गणित के निर्देश को "जॉम्बी" के रूप में जानने के लिए प्रेरित किया जाता है, जो कि परीक्षण पर सूत्र और एल्गोरिदम को थूकने की तुलना में थोड़ा अधिक सक्षम हैं।
एक ओर, हमारे पास "बुनियादी कौशल" का वास्तविक या कथित नुकसान है, आमतौर पर तुरंत याद के माध्यम से बहस में संकेत दिया जाता है, और दूसरी ओर, हमारे पास यह विचार है कि हमारे छात्र समस्या-समाधान के लिए पर्याप्त नहीं हैं "आधुनिक दुनिया", या "भविष्य" के लिए।
यह ध्यान देने योग्य है कि यह बहस कई पीढ़ियों पुरानी है।

A Modest Research Proposal for Mathematics Education

नीचे दी गई तस्वीर में दर्शाया गया भाव 1991 में प्रकाशित हुआ था। एक पीढ़ी बाद में, और हम अभी भी अटके हुए हैं, उसी बहस के कीचड़ में।
1989 से NCTM सुधार शुरू होने के बाद से गणित के शिक्षण और शिक्षण में कई तरह से प्रगति हुई है। यह 1960 के दशक के बाद से कई मायनों में आगे बढ़ गया है, जब पहले "New Mathematics" पाठ्यक्रम की कोशिश की गई थी (और अंततः छोड़ दिया गया था)। टिंकरिंग के एक सुसंगत मार्ग या यहां तक ​​कि असफल सुधार जैसा क्या लगता है, वास्तव में शिक्षण अभ्यास का एक निरंतर शोधन है। यह कहना है, पाठ्यक्रम और अभ्यास में सुधार सूक्ष्म है, लेकिन निरंतर है। खुद को सिखाना एक पुनरावृति कला है। ध्रुवीकरण नीतिवाद राजनीतिज्ञों के लिए है, शिक्षकों के लिए नहीं।
शिक्षक शिक्षण में सर्वश्रेष्ठ हैं। यह उनकी कला और शिल्प है। सीधे शब्दों में कहें: गणित का सन्निहित ज्ञान और इसे कैसे पढ़ाया जाता है यह लगातार विकसित हो रहा है और अपडेट हो रहा है, क्योंकि नए शिक्षक पेशे में प्रवेश करते हैं, और पुराने इसे छोड़ देते हैं। हालांकि, धीमी गति से परिवर्तन की एक स्थिर और स्थिर दर है। समय आगे बढ़ता है, और हम ऐसा करते हैं।
लेकिन शोध शिक्षण को सूचित कर सकता है। यह लेख भविष्य के प्रकार के अनुसंधान को आगे बढ़ाने का एक तरीका है जो गणित शिक्षा में शिक्षक अभ्यास को सूचित कर सकता है।

2.एक झूठी दिचोटॉमी?(A False Dichotomy?)-

एच। वू (1999) का एक दिलचस्प लेख "मिथ्या द्वंद्ववाद" के रूप में बुनियादी कौशल बनाम वैचारिक समझ बहस की विशेषता है।
एक लंबा उद्धरण इस बिंदु को बनाने में मदद करेगा:
गणित की शिक्षा में, यह बहस "बुनियादी कौशल या वैचारिक समझ" का रूप लेती है। यह फर्जी द्वंद्ववाद सार्वजनिक और शिक्षा समुदाय के एक वर्ग द्वारा आयोजित गणित की एक आम गलत धारणा से उत्पन्न होता है: सटीक और प्रवाह की मांग स्कूली गणित में बुनियादी कौशल के निष्पादन में वैचारिक समझ के अधिग्रहण के लिए काउंटर चलाता है। सच्चाई यह है कि गणित में, कौशल और समझ पूरी तरह से परस्पर जुड़े हुए हैं। ज्यादातर मामलों में, कौशल के निष्पादन में सटीकता और प्रवाह वैचारिक समझ को व्यक्त करने के लिए अपेक्षित वाहन हैं। एक तरफ "वैचारिक समझ" और दूसरी तरफ "समस्या-सुलझाने का कौशल" नहीं है।
लेखक स्पष्ट रूप से मिथक पर सवाल उठा रहा है, एक व्यापक, कि वैचारिक समझ * को पहले आना चाहिए। इस बात पर विचार करें कि दोनों प्रक्रियात्मक समझ (जिसे हम मोटे तौर पर "बुनियादी" कौशल कह सकते हैं) और वैचारिक समझ को आपस में जोड़ा गया है, या इंटरवॉवन-के रूप में रस्सी की मोटी ब्रैड में, जहां दोनों किस्में मूल रूप से एक साथ बुने जाते हैं।
यह मेरा विश्वास है कि शिक्षकों, शोधकर्ताओं और समाचार पत्रों के लिए लेख लिखने वालों को इस विश्वास को छोड़ने की जरूरत है कि एक को दूसरे से पहले होना चाहिए। भविष्य के शोध अध्ययन के अधिग्रहण का परीक्षण कर सकते हैं जिसे हम मोटे तौर पर "प्रक्रियात्मक स्थिति", और "वैचारिक स्थिति" कह सकते हैं।
आइए पाइथोगोरियन संबंधों को पढ़ाने का एक सरल उदाहरण दें।
छात्रों के दो समूहों पर विचार करें, निम्नलिखित दो निर्देशात्मक रास्ते नीचे जा रहे हैं।

3.निर्देशात्मक पथ एक(Instructional Path One)-

बोर्ड पर सूत्र नीचे लिखें। बताएं कि यह सूत्र कैसे काम करता है।
छात्रों को काम करने के लिए प्रश्नों का एक सेट दें। उन्हें दिखाओ कि कैसे कर्ण के समाधान के लिए काम करना है।
छात्रों को या तो पाद  के लिए हल करने से प्रश्न पूछें।
गलत धारणाओं और समस्याओं का समाधान करें।
छात्रों को अधिक जटिल समस्याएं दें, और उनकी समझ पर उनका मूल्यांकन करें।

4.निर्देशात्मक मार्ग दो(Instructional Path Two)-

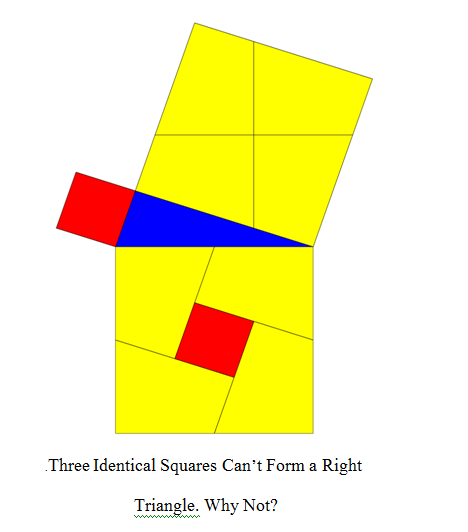
छात्रों को प्रमेय का ज्यामितीय प्रमाण दिखाएं। क्या उन्हें समकोण त्रिभुजों के भुजाओं से जोड़ते हैं। आपके द्वारा खोजे गए संबंध की जांच करें।
बीजगणित में अपने निष्कर्षों का अनुवाद करें। ज्यामितीय प्रतिनिधित्व द्वारा बनाई गई "चित्र" का अनुवाद बीजगणितीय रूप में किया जाता है।
छात्रों को फॉर्मूला काम करने का तरीका दिखाएं। उन्हें अभ्यास करने के लिए प्रश्न दें।
4. छात्रों को अधिक जटिल समस्याएं दें, और उनकी समझ पर उनका मूल्यांकन करें।
यहाँ पर्याप्त अंतर दूसरे पथ में ज्यामितीय तत्व है। लेकिन इस तत्व को पहले निर्देशात्मक मार्ग में काम किया जा सकता था, शायद बाद में।
आप अपने लिए यह तय कर सकते हैं कि निर्देशात्मक मार्ग में निम्नलिखित संकेत कहाँ हैं। शुरुआत की ओर? जब प्रमेय की खोज? या अंत में, छात्रों की सोच को आगे बढ़ाने के एक तरीके के रूप में, उन्हें बीजगणित में महारत हासिल करने के बाद?

A Modest Research Proposal for Mathematics Education

हमारा शोध प्रश्न यह हो सकता है: क्या छात्रों के ये दो समूह पाइथागोरस संबंध को एक ही तरह से और एक ही गहराई से समझ पाएंगे? यदि हम अपने शोध अध्ययन से एक ठोस निष्कर्ष निकाल सकते हैं, तो हम प्रक्रियात्मक या वैचारिक पक्ष पर उतर सकते हैं, और यदि नहीं, तो हम यह निष्कर्ष निकाल सकते हैं कि दोनों समूहों का समापन बिंदु लगभग बराबर है। यहां ध्यान देने योग्य बात: दोनों मार्गों में प्रक्रियात्मक और वैचारिक तत्व कहलाएंगे। उनके बीच आगे और पीछे असली है।

5.एक बैक-एंड-फोर्थ, या प्रक्रियात्मक और वैचारिक समझ के बीच परिवर्तन(A Back-and-Forth, or Iteration Between Procedural and Conceptual Understanding)-

यदि हम प्रक्रियात्मक समय की एक निश्चित अवधि में प्रक्रियात्मक और वैचारिक समझ के बीच आगे-पीछे, और आगे-पीछे जा रहे हैं, तो इन दोनों श्रेणियों के बीच कोई कठिन और तेज़ बाधाएँ नहीं हैं।
रिटल-जॉनसन, सीगलर, और अलीबली (2001) का एक पेपर इस बिंदु को मदद करता है, और संभवतः भविष्य के शोध के लिए आगे का रास्ता बताता है। वे ध्यान देते हैं कि आम तौर पर हम ज्ञान के एक "प्रकार" को दूसरे की मिसाल के रूप में देखते हैं। लेखकों का मानना ​​है कि ऐसा करने की आवश्यकता नहीं है, और यह ऐसा करने के लिए बेकार है:
इस पिछले शोध और सिद्धांत के विपरीत, हम प्रस्ताव करते हैं कि विकास के दौरान, वैचारिक और प्रक्रियात्मक ज्ञान एक दूसरे को प्रभावित करते हैं। विशेष रूप से, हम प्रस्ताव करते हैं कि वैचारिक और प्रक्रियात्मक ज्ञान पुनरावृत्त रूप से विकसित होते हैं, एक प्रकार के ज्ञान में वृद्धि के साथ दूसरे प्रकार के ज्ञान में वृद्धि होती है, जो पहले में नई वृद्धि को ट्रिगर करती है।
अध्ययन का डिज़ाइन (दो भागों में, n = 74, और n = 59) छात्रों को एक संख्या रेखा पर दशमलव अंश (1 के तहत दशमलव) रखने वाले छात्रों के लिए था। उन्होंने इस कार्य को प्रक्रियात्मक बताया। उनका निष्कर्ष यह था कि प्रक्रियात्मक ज्ञान ने वैचारिक ज्ञान को सूचित किया, और इसके विपरीत। सबसे रोमांचक बात यह है कि दोनों ही बेहतर समस्या प्रतिनिधित्व का समर्थन करते हैं।
प्रतिनिधित्व सोच का एक अधिनियमन है; छात्रों के पास गणितीय अवधारणाओं के बारे में सोचने के तरीके होने चाहिए। हमारा लक्ष्य सिर्फ एक प्रक्रिया को पूरा करने में सक्षम है, या सिर्फ गणित की अवधारणाओं के बारे में सामान्य तरीके से सोचने के लिए है। हमें अवधारणाओं को दुनिया में लाने की जरूरत है। जैसा कि लेखक ध्यान दें, डोमेन ज्ञान में कौशल और अवधारणा दोनों शामिल हैं।
अध्ययन इस विचार की ओर इशारा करता है कि प्रतिनिधित्व जटिल है। एक प्रक्रिया, उदाहरण के लिए, के बारे में सोचा जा सकता है, और यह समझा और प्रतिनिधित्व किया जा सकता है। एक प्रक्रिया को एक अवधारणा से पूरी तरह से अलग "चीज" के रूप में व्यवहार करना, उदाहरण के लिए, शायद एक बुरी चीज है। गुणन के लिए मानक एल्गोरिथ्म जगह मूल्य की धारणाओं, और आंशिक उत्पादों को लेने में बंधा हुआ है, जो तब कुल हैं। कोई कारण नहीं है कि इस प्रक्रिया को पढ़ाना एक पुनरावृत्ति प्रक्रिया-अवधारणा और कौशल हो सकता है जिसे हम "एल्गोरिथ्म सीखना" कहते हैं।
इस तरह के भविष्य के अध्ययन से यह पता लगाने की कोशिश की जा सकती है कि यह पुनरावृत्ति कैसे होती है। प्रक्रियाएं और अवधारणाएं एक साथ कैसे काम करती हैं, एक-दूसरे के खिलाफ नहीं? यह स्वीकार करना कि उन्हें एक-दूसरे के खिलाफ काम नहीं करना है, और वास्तव में, कि वे एक साथ काम कर सकते हैं और एक शुरुआत होगी।
गणितीय समझ बनाने के लिए प्रक्रियाएँ और अवधारणाएँ एक साथ कैसे काम करती हैं?
केवल सबसे कट्टर डाइकोटोमिस्ट इस बिंदु पर, इस बात को मानने से इंकार कर देगा कि आम जमीन है। यह इस आम जमीन पर है कि, एक दिन, "गणित  युद्धों" के युद्धविराम पर हस्ताक्षर किए जाएंगे। या, कम से कम, हमारे पास बेहतर और अधिक शोध होगा जो दर्शाता है कि आम जमीन पर मिलना भी संभव है।