Why We Rationalize The Denominator?

Why We Rationalize The Denominator

1.क्यों हम हर का परिमेयकरण करते हैं  का परिचय ??(Introduction of Why We Rationalize The Denominator?)-

इस आर्टिकल में बताया गया है कि व्यंजक का हर ऐसा अंक हो जिसका प्राकृत संख्या में वर्गमूल नहीं निकाला जा सकता हो तो उसके परिमेयकरण की आवश्यकता क्यों हैं और उसका क्या लाभ है? जबकि अंश में करणी चिन्ह में संख्या हो तो उसके परिमेयकरण की आवश्यकता नहीं होती है अथवा उसका परिमेयकरण नहीं करते हैं यदि करते हैं तो कब करते हैं? वास्तविक संख्याएँ दो प्रकार की होती है - (1.)परिमेय संख्याएँ (Rational Numbers) (2.)अपरिमेय संख्याएँ (Irrational Numbers)

(1.)परिमेय संख्याएँ (Rational Numbers) -

ऐसी संख्याएँ जो p/q के रूप में लिखी जा सकती हैं जहाँ p व q पूर्णांक हैं, दोनो का कोई उभयनिष्ठ गुणनखण्ड नहीं है तथा q शून्य नहीं है, परिमेय संख्याएँ कहलाती है।

(2.)अपरिमेय संख्याएँ (Irrational Numbers) -

ऐसी संख्याएँ जो परिमेय नहीं है अपरिमेय संख्याएँ कहलाती है।
√2=1.414213562.......
Pi =3.141592653.........
(3.)यदि दो परिमेय संख्याओं को जोड़ें, घटाएं, गुणा करें तब भी हमें एक अपरिमेय संख्या प्राप्त होती है (अर्थात् जोड़, घटाना, गुणा के सापेक्ष परिमेय संख्याएँ संवृत (closed) होती है। हालांकि अपरिमेय संख्याएँ भी योग और गुणन के क्रमविनिमेय, साहचर्य और बंटन नियमों को संतुष्ट करती है। परन्तु अपरिमेय संख्याओं के योग, अंतर. भागफल और गुणनफल सदा अपरिमेय नहीं होते हैं। इस प्रकार एक परिमेय संख्या में अपरिमेय संख्या जोड़ते हैं और एक परिमेय संख्या को एक अपरिमेय संख्या से गुणा करते हैं तो ये अपरिमेय संख्या होती है।
(4.)एक परिमेय संख्या और एक अपरिमेय संख्या का जोड़ या घटाने पर एक अपरिमेय संख्या प्राप्त होती है।
(5.)एक अपरिमेय संख्या के साथ एक शून्येत्तर (non-zero) परिमेय संख्या का गुणनफल या भागफल से एक अपरिमेय संख्या प्राप्त होती है।
(6.) यदि हम दो अपरिमेय संख्याओं को जोड़ें, घटाएँ, गुणा करें या एक अपरिमेय संख्या में दूसरी अपरिमेय संख्या का भाग दें तो परिणाम में परिमेय या अपरिमेय कुछ भी हो सकता है।

(7.)परिमेयकरण (rationalise) -

जब एक व्यंजक के हर में वर्गमूल वाला एक पद होता है या कोई संख्या करणी चिन्ह के अन्दर हो तब इसे तुल्य व्यंजक में हर को परिमेय संख्या में परिवर्तित करने की क्रियाविधि को हर का परिमेयकरण कहा जाता है।
(8.)हर का परिमेयकरण करने से व्यंजक का सरलीकरण हो जाता है जिससे हम उसका मान आसानी से निकाल सकते हैं। कभी-कभी अंश के परिमेयकरण से भी व्यंजक का सरलीकरण होता है और हम व्यंजक का मान आसानी से ज्ञात कर सकते हैं।
(9)अंश या हर का परिमेयकरण करने से अपरिमेय संख्या परिमेय संख्या में परिवर्तित हो जाती है जिससे व्यंजक का मान आसानी से ज्ञात किया जा सकता है।

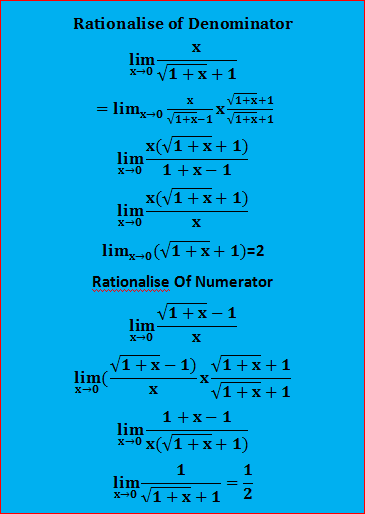Why We Rationalize The Denominator?

(10.)परिमेयकरण से बहुत बड़ी तथा अव्यवस्थित व्यंजक छोटे रूप में तथा व्यवस्थित रूप में हो जाता है जिससे उससे लिखने व पढ़ने में आसानी रहती है।
(11.)परिमेयकरण से व्यंजक संक्षिप्त हो जाता है और कहा भी गया है कि संक्षिप्त में अपनी बात को कहना या व्यक्त करना, वाक्य या भिन्नों की सुन्दरता को बढ़ाता है। व्यंजक को हल करने में रुचि व जिज्ञासा जाग्रत होती है जबकि जटिल व सम्मिश्र भिन्न अरुचिकर, बोझिल होता है।
(12.)यही कारण है कि किसी व्यंजक का परिमेयकरण किया जाता है या परिमेयकरण करने की आवश्यकता होती है। अक्सर कभी-कभी हम हमारे उत्तर को बिना परिमेयकरण के छोड़ देते हैं। विद्यार्थी अक्सर यही सवाल पूछते हैं कि बिना परिमेयकरण के उत्तर दे दिया जाए तो ठीक होगा या नहीं। उत्तर में निवेदन है कि परिमेयकरण से हमारे ज्ञान की गहराई तथा व्यापकता का पता चलता है इसलिए जहाँ तक हो सके परिमेयकरण करना चाहिए।
(13.)कई बार भिन्नों का मान अंनत या अपरिभाषित प्राप्त होता है परन्तु परिमेयकरण से  अंनत या अपरिभाषित की समस्या समाप्त हो जाती है। 
(14.)यदि यह आर्टिकल आपको पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें ।यदि आपकी कोई समस्या हो या कोई सुझाव हो तो कमेंट करके बताएं ।इस आर्टिकल को पूरा पढ़ें।

2.क्यों हम हर का परिमेयकरण करते हैं ??(Why We Rationalize The Denominator?)-

आपने इसे बार-बार सुना है, "भाजक को युक्तिसंगत बनाएँ। हर को तर्कसंगत बनाने के लिए सुनिश्चित करें! ”लेकिन क्यों ??? किसने तय किया कि मूल को भाजक से और अंश में से निकाला जाना है?आरटीडी अलजेब्रा से कैलकुलस तक मानक क्यों बने, इसके तीन कारण हैं।

3.कॉमन्सेंस कारण(Commonsense Reason)-

आरटीडी की आवश्यकता का मानक कारण पूरी तरह से व्यावहारिक है। जैसा कि आपने सबसे अधिक खोजा है, गणित में आप अक्सर कई अलग-अलग तरीकों और रूपों में समाधान लिख सकते हैं। ये सभी विविधताएं शांत हैं, लेकिन व्यावहारिक उद्देश्यों के लिए, वे आपके कागजात को ग्रेडिंग करने वालों के लिए जीवन को अधिक कठिन बनाते हैं।
उत्तरों के लिए एक मानक रूप को परिभाषित करना और आवश्यक करना आपके शिक्षक को यह सत्यापित करने के लिए समय लेने वाला सिरदर्द बचाता है कि आपका समाधान उत्तर कुंजी के बराबर है, या इससे भी बदतर, गलती से आपके उत्तर को गलत चिह्नित कर रहा है!
जैसे एक अंश को उसके सरलतम रूप में कम करने के लिए, आरटीडी, हर में वर्गमूल  के साथ अंशों को सरल बनाने के लिए प्रोटोकॉल है।

4.उचित कारण(Reasonable Reason)-

एक सामान्य रूप से परिभाषित नामकरण समझ में आता है और सभी, लेकिन फिर भी हमें इस सवाल के साथ छोड़ देता है: हमने क्यों तय किया है कि अंश में वर्गमूल  होना ठीक है, लेकिन हर  में वर्गमूल नहीं है ??
(2√3) / 3  को 2 / √3 का सरल रूप क्यों कहा जाता है?
कारण यह है कि अगर हमें रेडिकल के साथ अंश जोड़ना या घटाना है, तो यह गणना करना आसान है कि तर्कहीन संख्याओं के बजाय हर में पूर्ण संख्याएं हैं। उदाहरण के लिए, गैर-तर्कसंगत संस्करण की तुलना में (2√3 / 3) + ((3 -√ )2) / 7) जोड़ना आसान है: (2 / √3) + (1 / (3 + √2)।
अंशों के पहले सेट को एक साथ जोड़ने के लिए हम सभी को 21 का एक सामान्य भाजक बनाना होगा और फिर अंशों से शब्दों को जोड़ना होगा। यह लगभग स्पष्ट नहीं है कि आम भाजक भिन्न के दूसरे सेट का क्या है।
दूसरी समस्या को हल करने के लिए, आप सबसे पहले हर को युक्तिसंगत बनाने की कोशिश करेंगे और फिर एक साथ फ्रैक्चर को जोड़ने से पहले 21 के सामान्य हर को बनाएं।
इसलिए RTD समाधानों की तुलना और ग्रेडिंग के लिए एक सामान्य रूप प्रदान करता है और साथ ही जरूरत पड़ने पर हाथ से आगे की गणना करना हमारे लिए आसान बनाता है।

5.ऐतिहासिक कारण(Historical Reason)-

इस बिंदु पर आप सोच रहे होंगे, "क्यों न केवल वर्गमूल  को वर्गमूल  में छोड़ दिया जाए और उन्हें तब और युक्तिसंगत बनाया जाए जब मुझे भिन्नों को जोड़ने या घटाने की आवश्यकता होती है?"
और हाँ, यह एक वैध बिंदु है। यही कारण है कि शायद हम आरटीडी के लिए अक्सर ऐसा क्यों करते हैं, इसका सबसे अच्छा जवाब ऐतिहासिक है। उत्तर जो हमें कंप्यूटर और कैलकुलेटर से पहले जीवन में वापस ले जाता है, सर्वव्यापी थे। वापस जब लोगों को नियमित रूप से विभाजन करना पड़ा ... हाथ से! * दम तोड़ देना! *
चलो ऊपर से हमारे दो समकक्ष अंशों पर एक नज़र डालें:
यदि हम वास्तव में इन अंशों को विभाजित करना चाहते हैं तो क्या होगा?
आइए हाथ से 2/√3  विभाजित करके शुरुआत करें।
कैलकुलेटर से पहले, आप हाथ से√3   के एक अनुमान को खोजने के लिए एक एल्गोरिथ्म का उपयोग करके शुरू करेंगे, जो कि 1.73205081 है ... √3 को अनुमानित करने के बाद, आप फिर अपना लंबा विभाजन सेट करेंगे।
यदि यह आपको जटिल लगता है, तो इसका कारण यह है। एक तर्कहीन संख्या होने के कारण विभाजक व्यावहारिक रूप से अनसुना है।
इस विभाजन को करने के लिए, आपको यह तय करना होगा कि आप कितने दशमलव स्थानों को अपने आस-पास रखना चाहते हैं, उस दशमलव स्थान पर चक्कर लगाना चाहते हैं, फिर आपको अपने भाजक को बनाने के लिए लाभांश और भाजक दोनों को दस की बड़ी शक्ति से गुणा करना होगा। एक पूरी संख्या। वह सब करने के बाद आप उन दो अनिर्दिष्ट संख्याओं को विभाजित करने के गन्दे कार्य के साथ आगे बढ़ सकते हैं।
अब इस बात पर एक नज़र डालते हैं कि हम समतुल्य, परिमेय अंश को विभाजित करने के बारे में कैसे जानते हैं: (2√3) / 3।
कैलकुलेटर के बिना, आप उपरोक्त √3 के लिए सन्निकटन की गणना करके शुरू करते हैं, जो कि 1.73205081 है… अगला, आपने 1.73205081… 2 से गुणा करके 3.46410162 प्राप्त किया… फिर बस अपना विभाजन सेट करें।
यह हाथ से विभाजित करने के लिए बहुत आसान है! हमें कोई भी पूर्व काम नहीं करना है, हम सीधे विभाजन समस्या में कूद सकते हैं।

6.और सबसे महत्वपूर्ण बात, आरटीडी के लिए कैसे :(And most importantly, HOW to RTD )-

अब जब आप समझ गए हैं कि RTD के लिए यह इतना महत्वपूर्ण क्यों है, तो आप इस पर अभ्यास करना चाहते हैं!
यह पहला ट्यूटोरियल बताता है कि मानक वर्ग मूल के साथ भाजक को कैसे युक्तिसंगत बनाया जाए, तब प्रदर्शित करने के लिए चाल को दर्शाता है कि भाजक के परिमेय परिदृश्य को कैसे संभालें जब आपके पास एक पूर्ण संख्या का योग या अंतर हो और भाजक में एक वर्गमूल हो। ऐसा करने के लिए आपको संयुग्म से परिचित कराया जाएगा।
इस दूसरे ट्यूटोरियल में, आप सीखेंगे कि घनमूल और चतुर्थमुल  के साथ अधिक कठिन हर को कैसे युक्तिसंगत बनाया जाए। हम इस बारे में भी बात करेंगे कि प्रक्रिया को सरल बनाने के लिए आप वैकल्पिक भिन्नात्मक घातांक संकेतन का उपयोग कैसे कर सकते हैं।
अधिक गणित सहायता की आवश्यकता है?
बीजगणित, त्रिकोणमिति, Precalculus, कलन , और उन्नत गणित से लोकप्रिय विषयों को कवर करने वाले अधिक हाथों के गणित के ट्यूटोरियल के लिए ब्लॉग के अन्य आर्टिकल पर गणित भाड़े की जांच करें।
आप कई सारे इंटरस पा सकते हैं...