Black-Scholes formula, explained

1.ब्लैक-स्कोल्स सूत्र का परिचय (Introduction of Black-Scholes formula)-

ब्लैक होल्स माॅडल गणितीय रूप से बाजार कैसे कार्य करता है के बारे में बताता है। बाजार में वस्तुओं के मूल्यों के उतार-चढ़ाव को क्या-क्या प्रभावित करता है। विकल्प, वायदा आगे और स्वैप के साथ अनुकरण करता है ।मान्यता है कि स्टाॅक अनिवार्य रूप से जोखिम मुक्त संपत्ति है।इस आर्टिकल में ब्लैक हॉल सूत्र ,ब्लैक स्कोल्स मॉडल ,

मान्यताएँ जिनमें शामिल है 1. जोखिम मुक्त संपत्ति पर वापसी की दर स्थिर है (इस प्रकार प्रभावी रूप से ब्याज दर के रूप में व्यवहार करता है); 2. जोखिमपूर्ण संपत्ति की कीमत का तात्कालिक लॉग रिटर्न ज्यामितीय ब्राउनियन गति के अनुसार, निरंतर बहाव और अस्थिरता के साथ एक असीम यादृच्छिक चलने के रूप में व्यवहार करने के लिए माना जाता है। 3. जोखिम भरी संपत्ति लाभांश का भुगतान नहीं करती है।

ब्लैक-स्कोल्स समीकरण,ब्लैक-स्कोल्स फॉर्मूला ,उदाहरण: एक यूरोपीय कॉल विकल्प की कीमत की गणना,

अंतर्निहित अस्थिरता,अमेरिकी विकल्प के बारे में बताया गया है। इस आर्टिकल को पूरा पढ़ें और पसन्द आए तो लाभ उठाए। इसे अपने मित्रो के साथ शेयर करे और लाईक करे। यदि कोई सुझाव हो तो इसे पसन्द करें। 

 2.ब्लैक-स्कोल्स सूत्र, समझाया(Black-Scholes formula, explained)-

वित्त में सबसे प्रसिद्ध समीकरण का परिचय
ब्लैक-स्कोल्स मॉडल एक गणितीय मॉडल है जो व्युत्पन्न वित्तीय साधनों वाले वित्तीय बाजार की गतिशीलता का अनुकरण करता है। १ ९ s३ में इसकी शुरुआत और १ ९ and० और estim० के दशक में शोधन के बाद से, मॉडल यूरोपीय-शैली स्टॉक विकल्पों की कीमत का आकलन करने के लिए वास्तविक मानक बन गया है। मॉडल के पीछे मुख्य विचार निवेश पोर्टफोलियो में विकल्पों को हेज करना है और अंतर्निहित संपत्ति (जैसे स्टॉक) को सही तरीके से खरीदकर और बेचकर, परिणामस्वरूप, जोखिम को खत्म करना है। विधि को बाद में वित्त के भीतर "लगातार संशोधित हेजिंग" के रूप में जाना जाता है, और दुनिया के कई अग्रणी निवेश बैंकों और हेज फंडों द्वारा अपनाया गया है।
इस लेख का लक्ष्य ब्लैक-स्कोल्स समीकरण के गणितीय आधार, अंतर्निहित मान्यताओं और निहितार्थों की व्याख्या करना है।
पढ़ने का आनंद लो!

3.ब्लैक-स्कोल्स मॉडल(The Black-Scholes model)-

ब्लैक-स्कोल्स मॉडल एक गणितीय मॉडल है जो एक वित्तीय बाजार की गतिशीलता को व्युत्पन्न वित्तीय साधनों जैसे कि विकल्प, वायदा, आगे और स्वैप के साथ अनुकरण करता है। मॉडल की प्रमुख गुणधर्म  यह है कि यह दर्शाता है कि अंतर्निहित सुरक्षा के जोखिम और इसकी अपेक्षित वापसी की परवाह किए बिना एक विकल्प की एक अद्वितीय कीमत है। मॉडल एक आंशिक अंतर समीकरण (पीडीई), तथा कथित ब्लैक-स्कोल्स समीकरण पर आधारित है, जिसमें से ब्लैक-स्कोल्स फॉर्मूला को घटाया जा सकता है, जो यूरोपीय स्टॉक विकल्पों की सही कीमत का सैद्धांतिक अनुमान देता है।

4.मान्यताओं(Assumptions)-

मूल ब्लैक-स्कोल्स मॉडल एक मुख्य धारणा पर आधारित है कि बाजार में कम से कम एक जोखिमपूर्ण संपत्ति (जैसे स्टॉक) और एक (अनिवार्य रूप से) जोखिम मुक्त संपत्ति होती है, जैसे कि मनी मार्केट फंड, नकद या सरकारी बॉन्ड। । इसके अलावा, यह दो परिसंपत्तियों के तीन गुणों को मानता है, और बाजार के चार:
बाजार में परिसंपत्तियों के बारे में अनुमान हैं: 1. जोखिम मुक्त संपत्ति पर वापसी की दर स्थिर है (इस प्रकार प्रभावी रूप से ब्याज दर के रूप में व्यवहार करता है); 2. जोखिमपूर्ण संपत्ति की कीमत का तात्कालिक लॉग रिटर्न ज्यामितीय ब्राउनियन गति के अनुसार, निरंतर बहाव और अस्थिरता के साथ एक असीम यादृच्छिक चलने के रूप में व्यवहार करने के लिए माना जाता है। 3. जोखिम भरी संपत्ति लाभांश का भुगतान नहीं करती है।
बाजार के बारे में अनुमान ही हैं: 1. कोई मध्यस्थता (जोखिम-मुक्त लाभ) के अवसर नहीं हैं; 2. जोखिम मुक्त संपत्ति की ब्याज दर के रूप में उसी दर पर किसी भी राशि को उधार लेना और उधार देना संभव है; 3. स्टॉक की किसी भी राशि को खरीदना और बेचना संभव है (शॉर्ट सेलिंग सहित); और 4. बाजार में कोई लेनदेन लागत नहीं है (यानी प्रतिभूतियों या व्युत्पन्न उपकरणों को खरीदने या बेचने के लिए कोई कमीशन नहीं)।
मूल मॉडल के बाद के विस्तार में, इन धारणाओं को जोखिम-मुक्त संपत्ति (मर्टन, 1976) के लिए गतिशील ब्याज दरों के लिए समायोजित करने के लिए संशोधित किया गया है, खरीदने और बेचने के लिए लेनदेन लागत (इंगरसोल, 1976) और जोखिम परिसंपत्ति (लाभांश) के लिए लाभांश भुगतान व्हेल, 1981)। इस निबंध में, मान लें कि हम मूल मॉडल के साथ काम कर रहे हैं, जब तक कि अन्यथा न कहा जाए।

5.ब्लैक-स्कोल्स समीकरण(The Black-Scholes equation)-

चित्र 1. ब्लैक-स्कोल्स समीकरण का उपयोग करके परिकलित मूल्य और स्टॉक मूल्य के संबंध में यूरोपीय कॉल विकल्प मूल्य / मूल्य का ग्राफिक प्रतिनिधित्व
ब्लैक-स्कोल्स समीकरण आंशिक अंतर समीकरण (PDE) है जो ब्लैक-स्कोल्स (कभी-कभी ब्लैक-स्कोल्स-मर्टन) मॉडल की गतिशीलता के अनुसार संचालित होने वाले वित्तीय बाजारों में यूरोपीय स्टॉक विकल्पों के मूल्य विकास को नियंत्रित करता है। समीकरण है:

Black-Scholes formula, explained

समीकरण 1. ब्लैक-स्कोल्स आंशिक अंतर समीकरण जो एक यूरोपीय कॉल की कीमत का वर्णन करता है या समय के साथ विकल्प रखता है
जहां V विकल्प की कीमत है (दो चर के एक समारोह के रूप में: शेयर की कीमत एस और समय टी), आर जोखिम-मुक्त ब्याज दर है (उस पर ब्याज दर के समान सोचें जो आपको मनी-मार्केट फंड से प्राप्त होगी। , जर्मन सरकारी ऋण या समान "सुरक्षित" ऋण प्रतिभूतियां) और अंतर्निहित सुरक्षा के लॉग रिटर्न की अस्थिरता है (इस लेख के प्रयोजनों के लिए, हम स्टॉक पर विचार कर रहे हैं)। जॉन सी। हल के "विकल्प, फ्यूचर्स एंड अदर डेरिवेटिव्स" (1989) के आधार पर, विकिपीडिया पर समीकरण का एक साफ व्युत्पत्ति उपलब्ध है।
यदि हम निम्नलिखित फॉर्म में समीकरण को फिर से लिखते हैं

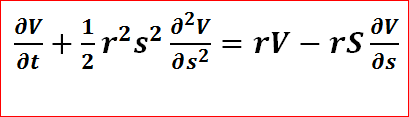Black-Scholes formula, explained

समीकरण 2. ब्लैक-स्कोल्स समीकरण का पुनर्निर्मित रूप
फिर बाईं ओर विकल्प  के मूल्य / मूल्य में समय-समय पर होने वाले बदलाव को दर्शाता है + स्टॉक की कीमत के सापेक्ष विकल्प के मूल्य की उत्कर्षता। दाहिने हाथ की ओर विकल्प में लंबी स्थिति से जोखिम मुक्त रिटर्न का प्रतिनिधित्व करता है और स्टॉक के V / .S शेयरों से मिलकर एक छोटी स्थिति होती है। ग्रीक्स के संदर्भ में:
समीकरण 3. थीटा (Θ) + गामा (=) = (जोखिम-मुक्त दर) x (विकल्प की कीमत) - (जोखिम-मुक्त दर) x (स्टॉक की कीमत) x Delta (Δ)

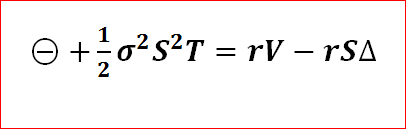Black-Scholes formula, explained

ब्लैक एंड स्कोल्स (1973) का मुख्य अवलोकन यह था कि किसी भी अपरिमित समय अंतराल पर स्टॉक और विकल्पों के संयुक्त पोर्टफोलियो का जोखिम मुक्त रिटर्न, थीटा (Θ) और एक टर्म के योग के रूप में व्यक्त किया जा सकता है। गामा (Γ)। अवलोकन को कभी-कभी "जोखिम तटस्थ तर्क" के रूप में जाना जाता है। इसका कारण यह है कि थीटा (Θ) का मान आम तौर पर नकारात्मक होता है (क्योंकि समय के समाप्त होने के साथ ही विकल्प का मूल्य कम हो जाता है) और गामा (Γ) का मूल्य आम तौर पर सकारात्मक होता है (विकल्प को पकड़े रहने से पोर्टफोलियो को मिलने वाले लाभ को दर्शाता है) । संक्षेप में, थीटा से नुकसान और गामा से लाभ एक दूसरे को ऑफसेट करते हैं, जिसके परिणामस्वरूप जोखिम-मुक्त दर पर रिटर्न मिलता है।

6.ब्लैक-स्कोल्स फॉर्मूला(The Black-Scholes formula)-

ब्लैक-स्कोल्स फॉर्मूला ब्लैक-स्कोल्स पीडीई का एक समाधान है, जिसे नीचे दी गई सीमा की स्थिति (eq। 4 और 5) दिया गया है। यह यूरोपीय पुट और कॉल विकल्पों की कीमत की गणना करता है। यही है, यह भविष्य में पूर्व निर्धारित तिथि पर पूर्व-निर्धारित मूल्य पर कुछ अंडरलेइंग एसेट खरीदने या बेचने के अधिकार (लेकिन दायित्व नहीं) के अनुबंध की कीमत की गणना करता है। परिपक्वता / समाप्ति (टी) पर, ऐसे यूरोपीय कॉल (C) और पुट (P) विकल्पों का मूल्य क्रमशः दिया जाता है:

Black-Scholes formula, explained

यूरोपीय कॉल विकल्प के मूल्य / मूल्य के लिए समीकरण 4

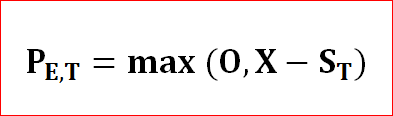Black-Scholes formula, explained

यूरोपीय पुट ऑप्शन के मूल्य / मूल्य के लिए समीकरण 5
ब्लैक एंड स्कोल्स ने दिखाया कि ब्लैक-स्कोल्स समीकरण (eq 1 ऊपर) के विश्लेषणात्मक समाधान का कार्यात्मक रूप समीकरण  द्वारा दी गई सीमा शर्तों के साथ है। यूरोपीय कॉल विकल्प के लिए 4 और 5 है:

Black-Scholes formula, explained

समीकरण 6. मूल्य के स्टॉक के गैर-लाभांश भुगतान वाले स्टॉक के लिए कॉल विकल्प सी के मूल्य के लिए

7.ब्लैक-स्कोल्स फॉर्मूला(The Black-Scholes formula)-

सूत्र गैर-लाभांश-भुगतान वाले स्टॉक के लिए यूरोपीय कॉल विकल्पों का मूल्य / मूल्य देता है। सूत्र में जाने वाले कारक S = सुरक्षा की कीमत, समाप्ति की तिथि, T = वर्तमान तिथि, t = वर्तमान तिथि, X = व्यायाम मूल्य, r = जोखिम-मुक्त ब्याज दर और vol = अस्थिरता (अंतर्निहित संपत्ति का मानक विचलन) हैं। फ़ंक्शन N (function) एक सामान्य (गाऊसी) वितरण के लिए संचयी वितरण फ़ंक्शन का प्रतिनिधित्व करता है और of संभावना के रूप में सोचा जा सकता है कि एक यादृच्छिक चर कम या इसके इनपुट के बराबर है (यानी सामान्य वितरण के लिए d₁ और d ’)’। प्रायिकता होने के नाते, दूसरे शब्दों में मान N (the) का मान हमेशा 0 (N (・) के बीच होगा। 1. इनपुट d≤ और d₂ द्वारा दिए गए हैं:

Black-Scholes formula, explained

समीकरण 7
बहुत अनौपचारिक रूप से, ब्लैक-स्कोल्स फॉर्मूले द्वारा दिए गए योग में दो शब्दों को 'संभावना के भारित स्टॉक की मौजूदा कीमत के रूप में सोचा जा सकता है कि आप स्टॉक को खरीदने के लिए अपने विकल्प का प्रयोग करेंगे' एक्सरसाइज की रियायती कीमत विकल्प संभावना द्वारा भारित होता है कि आप विकल्प का प्रयोग करेंगे ', या बस' आप क्या करने जा रहे हैं 'ऋण' क्या आप भुगतान करने जा रहे हैं '(खान, 2013)।
एक यूरोपीय पुट ऑप्शन के लिए (सही के लिए अनुबंध, लेकिन दायित्व नहीं, भविष्य में पूर्व निर्धारित तिथि पर पूर्व निर्धारित मूल्य पर कुछ अंडरलेइंग एसेट बेचने के लिए) समतुल्य कार्यात्मक रूप है:

Black-Scholes formula, explained

समीकरण 9. मूल्य-वर्ग के गैर-लाभांश भुगतान वाले स्टॉक के लिए पुट ऑप्शन C के मूल्य के लिए ब्लैक-स्कोल्स फॉर्मूला

8.उदाहरण: एक यूरोपीय कॉल विकल्प की कीमत की गणना(Example: Calculating the price of a European call option)-

यूरोपीय कॉल विकल्प की कीमत क्या होनी चाहिए, इसकी गणना करने के लिए, हमें पता है कि हमें समीकरण 6 के लिए आवश्यक पाँच मान चाहिए। वे हैं: 1. स्टॉक की मौजूदा कीमत (एस), 2. कॉल विकल्प (एक्स) का व्यायाम मूल्य, 3. समाप्ति का समय (टी - टी), 4. जोखिम-मुक्त ब्याज दर (आर) ) और 5. ऐतिहासिक लॉग रिटर्न (σ) के मानक विचलन द्वारा दिए गए स्टॉक की अस्थिरता।
टेस्ला (TSLA) के लिए कॉल विकल्प के मूल्य का अनुमान लगाना
पहले चार मूल्यों की हमें आसानी से प्राप्य है।
बता दें कि हम टेस्ला के स्टॉक ($ TSLA) के लिए एक कॉल विकल्प में रुचि रखते हैं, 2019 में अपनी Q3 की कमाई के दिन को परिपक्व करते हुए, वर्तमान में ट्रेडिंग की तुलना में 20% अधिक कीमत पर। आज (13 जुलाई, 2019) याहू वित्त पर टेस्ला की NASDAQ लिस्टिंग ($ TSLA) को देखते हुए, हम S = $ 245 का स्टॉक मूल्य पाते हैं। मौजूदा मूल्य को 1.2 के साथ गुणा करने से हमें व्यायाम मूल्य 20% अधिक मिलता है जो वर्तमान में कारोबार कर रहा है, एक्स = $ 294। Googling, हम पाते हैं कि इसकी Q3 आय कॉल का दिन 22 अक्टूबर है, जो हमें 22 अक्टूबर को समाप्त होने / परिपक्व होने का समय देता है - 13 जुलाई = 101 दिन। जोखिम-मुक्त ब्याज दर साधन के लिए एक प्रॉक्सी के रूप में, हम वर्तमान में 2.12% का भुगतान करके यूएस 10-वर्ष के सरकारी बॉन्ड (USGG10YR) का उपयोग करेंगे।
तो, हम S = 245, X = 294, T - t = 101 और r = 0.0212 पाते हैं। एकमात्र अनुपलब्ध मूल्य स्टॉक की अस्थिरता (।) का अनुमान है।
यदि हम जानते हैं कि वे अलग-अलग परिपक्वता / समाप्ति तिथियों (टी) और व्यायाम / हड़ताल की कीमतों (एक्स) पर एक ही स्टॉक के लिए अन्य विकल्प कीमतों की गणना करके, किसी भी स्टॉक की अस्थिरता का अनुमान लगा सकते हैं, या, और भी सरल। एक ब्लैक-स्कोल्स मॉडल के अनुसार सेट।

9.अंतर्निहित अस्थिरता(Implied volatility)-

हालांकि यह समझना दिलचस्प है कि कैसे जारीकर्ता अपने कॉल की कीमत पर पहुंचते हैं और विकल्प डालते हैं, क्योंकि निवेशकों के लिए ऐसी कीमतों, प्रति सेगमेंट के साथ "असहमत" होना मुश्किल है, और इसलिए इस ज्ञान को कार्रवाई योग्य निवेश शोध में बदलना मुश्किल है।
हालांकि हम ब्लैक-स्कोल्स फॉर्मूले से बहुत अधिक लाभ प्राप्त कर सकते हैं यदि हम इसके बजाय एक विकल्प की कीमत (सी या पी) को एक ज्ञात मात्रा / स्वतंत्र चर के रूप में मानते हैं (विभिन्न परिपक्वता / समाप्ति तिथियों को देखते हुए टी और अलग व्यायाम कीमतें एक्स)। ऐसा इसलिए है, क्योंकि अगर हम करते हैं, तो ब्लैक-स्कोल्स कार्यात्मक समीकरण हमें यह समझने में मदद करने के लिए एक उपकरण बन जाता है कि बाजार किसी शेयर की अस्थिरता का अनुमान कैसे लगाता है, जिसे विकल्प की निहित अस्थिरता भी कहा जाता है। यह ऐसी जानकारी है जिससे हम असहमत हैं, और इसके खिलाफ व्यापार कर सकते हैं।
यदि हम उदाहरण के लिए पिछले तीन महीनों (आंकड़ा 2) से अधिक टेस्ला स्टॉक के चार्ट को देखते हैं, तो हम $ 280 तीन महीने पहले लगभग $ 280 में हॉवरिंग से एक बल्कि (एक बेहतर शब्द की कमी के लिए) अस्थिर यात्रा देखते हैं। एक महीने पहले, अब $ 245 पर वापस आने के लिए। इससे समझ में आता है कि हमने पहले ($ 280- $ 180 = $ 100, $ 100/280 = 0.36, बनाम 0.38 डॉलर) की कीमतों से देखी गई अस्थिरता को देखते हैं। यह समझ में नहीं आता है, हालांकि, अगर हमें लगता है कि पिछले तीन महीनों में उतार-चढ़ाव एक हिमशैल का मात्र टिप था, टेस्ला के लिए अधिक अस्थिरता की अवधि में जा रहा है, कहते हैं, शॉर्ट-सेलिंग में आगामी वृद्धि के कारण।
चित्रा 2. $ TSLA के लिए 3 महीने का चार्ट
बता दें कि हम पिछले तीन महीनों में स्टॉक के प्रदर्शन की निहित अस्थिरता के बारे में एक विकल्प जारीकर्ता से असहमत हैं। हमें लगता है कि सवारी चट्टानी होने जा रही है। कितना? बता दें कि 40% के बजाय, हमें लगता है कि अगले तीन महीने 60% से अधिक लगेंगे। एस, एक्स, आर, और टी - टी के लिए समान मूल्यों के साथ कार्यात्मक ब्लैक-स्कोल्स सूत्र में इनपुट, हम विकल्प जारीकर्ता के लिए सी (एस, टी) = $ 14.32 पर लगभग दोगुना मूल्य प्राप्त करते हैं। यह हम व्यापार कर सकते हैं। उदाहरण के लिए, हम आज कॉल ऑप्शन खरीद सकते हैं और लाभ पर बेचने से पहले शेयर के मूल्य में वृद्धि या अस्थिरता की प्रतीक्षा कर सकते हैं।

10.अमेरिकी विकल्प(American options)-

चूँकि समाप्ति से पहले किसी भी तारीख को अमेरिकी विकल्पों का उपयोग किया जा सकता है (तथाकथित "निरंतर समय-साधन"), वे उस यूरोपीय विकल्प ("समय के साधनों में बिंदु") से निपटने के लिए बहुत अधिक कठिन हैं। मुख्य रूप से, चूंकि इष्टतम व्यायाम नीति विकल्प के मूल्य को प्रभावित करेगी, इसलिए ब्लैक-स्कोल्स के आंशिक समीकरण को हल करते समय इसे ध्यान में रखा जाना चाहिए। ब्लैक-स्कोल्स समीकरण के अनुसार अमेरिकी विकल्पों के लिए कोई ज्ञात "बंद फ़ॉर्म" समाधान नहीं हैं। हालांकि, कुछ विशेष मामले हैं:
अंतर्निहित परिसंपत्तियों पर अमेरिकी कॉल विकल्पों के लिए जो लाभांश (या अन्य भुगतान) का भुगतान नहीं करते हैं, अमेरिकी कॉल विकल्प मूल्य यूरोपीय विकल्प विकल्पों के समान है। ऐसा इसलिए है क्योंकि इस मामले में इष्टतम व्यायाम नीति विकल्प का प्रयोग नहीं करना है।
अंतर्निहित परिसंपत्तियों पर अमेरिकी कॉल विकल्पों के लिए जो अपने जीवनकाल में एक ज्ञानी व्यक्ति का भुगतान करते हैं, यह विकल्प को जल्दी व्यायाम करने के लिए इष्टतम हो सकता है। ऐसे मामलों में स्टॉक के पूर्व-लाभांश होने से ठीक पहले विकल्प का बेहतर इस्तेमाल किया जा सकता है, तथाकथित रोल-गेसके-व्हेल विधि (रोल, 1977; गेसके; 1979; 1981; 1981; क्लो-फॉर्म) द्वारा दिए गए समाधान के अनुसार। , 1981):
पहले, जाँच लें कि क्या यह विकल्प को जल्दी पूरा करने के लिए इष्टतम है, यह जाँच कर कि क्या निम्न असमानता पूरी हुई है:

Black-Scholes formula, explained

समीकरण 10।
एस = स्टॉक मूल्य, एक्स = व्यायाम मूल्य, डी divid = लाभांश भुगतान, टी = वर्तमान तिथि, लाभांश भुगतान की तिथि, टी = विकल्प की समाप्ति तिथि।
यदि असमानता पूरी नहीं होती है, तो प्रारंभिक व्यायाम इष्टतम नहीं है। यदि C (formula) गैर-लाभांश-भुगतान वाले स्टॉक (eq x) पर यूरोपीय कॉल विकल्पों के लिए नियमित ब्लैक-स्कोल्स फॉर्मूला है, तो अमेरिकी कॉल विकल्प का मूल्य उसी समीकरण के एक संस्करण द्वारा दिया जाता है जहां स्टॉक मूल्य ( एस) छूट है:

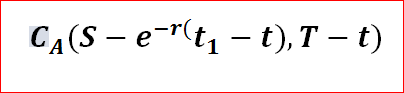Black-Scholes formula, explained

समीकरण 11. असमानता (eq.8) को पूरा करने पर एक अमेरिकी कॉल विकल्प का मूल्य पूरा नहीं होता है
यदि असमानता पूरी हो जाती है, तो प्रारंभिक व्यायाम इष्टतम है और अमेरिकी कॉल विकल्प का मूल्य निम्नलिखित, भयानक, एक समीकरण की गड़बड़ी द्वारा दिया जाता है (मैंने इसे अधिक पठनीय बनाने के लिए प्रत्येक शब्द द्वारा इसे तोड़ने की कोशिश की:)

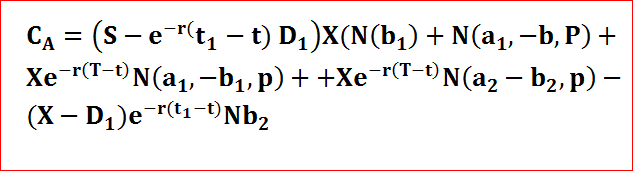Black-Scholes formula, explained

समीकरण 12. असमानता (eq। 10) पूरा होने पर एक अमेरिकी कॉल विकल्प का मूल्य
जहां एस = स्टॉक की कीमत से पहले, विकल्प की समाप्ति की तारीख = तिथि = एक्स = व्यायाम की कीमत और आर = जोखिम-मुक्त ब्याज दर, rate = अस्थिरता (स्टॉक के ऐतिहासिक रिटर्न के लॉग का मानक विचलन), और डी price लाभांश भुगतान है। इसके अलावा, ρ द्वारा दिया जाता है:

 समीकरण 13।
a₂, a₁ द्वारा:
समीकरण 14।
समीकरण 15।
और b and, b₁ द्वारा:
समीकरण 16।
समीकरण 17।
11.सीमाएं(Limitations)-
यह कहे बिना जाना चाहिए कि ब्लैक-स्कोल्स मॉडल ठीक है कि, एक सैद्धांतिक मॉडल जो यह अनुमान लगाने की कोशिश करता है कि बाजार कैसे व्यवहार करता है, ऊपर बताई गई मान्यताओं और जोखिम मुक्त ब्याज दरों (आर) के हमारे अपने संख्यात्मक अनुमानों की अंतर्निहित सीमा को देखते हुए। भविष्य की अस्थिरता (σ)। यहां यह रेखांकित किया जाना चाहिए कि सभी की धारणाएं (विशेष रूप से मूल) नहीं हैं.
यहां यह रेखांकित किया जाना चाहिए कि सभी की धारणाएं (विशेष रूप से मूल मॉडल) वास्तव में अनुभवजन्य रूप से मान्य नहीं हैं। उदाहरण के लिए, महत्वपूर्ण सीमाएँ इससे उत्पन्न होती हैं:
स्टॉक में अत्यधिक चालों का कम आंकना, पूंछ के जोखिम को कम करना
तत्काल, लागत-कम व्यापार की धारणा, तरलता जोखिम का उत्पादन
एक स्थिर प्रक्रिया की धारणा, अस्थिरता जोखिम की उपज
निरंतर समय और व्यापार की धारणा, उपज जोखिम
उदाहरण के लिए, किसी भी और सभी निवेश रणनीतियों के लिए जिम्मेदार होना चाहिए, उदाहरण के लिए आउट-ऑफ-द-मनी विकल्पों के साथ हेजिंग, कई एक्सचेंजों पर व्यापार, क्रमशः अस्थिरता हेजिंग और गामा हेजिंग के साथ हेजिंग।

12.पृष्ठभूमि(Background)-

जैसा कि संक्षेप में उल्लेख किया गया था कि यह फिशर ब्लैक और माय्रोन स्कोल्स था जिन्होंने 1973 में दिखाया था कि कुछ नियमों के अनुसार गतिशील रूप से एक पोर्टफोलियो को संशोधित करना अंतर्निहित सुरक्षा (ब्लैक एंड स्कोल्स, 1973) की अपेक्षित वापसी को हटा देता है। उनका मॉडल पहले से स्थापित कामों पर बेकलियर, कसौफ, थोरो और अन्य द्वारा बनाया गया है। रॉबर्ट सी। मर्टन ने मॉडल की समझ पर विस्तार करते हुए एक पेपर प्रकाशित किया था और जिसने "ब्लैक-स्कोल्स ऑप्शंस प्राइसिंग मॉडल" शब्द को गढ़ा था। स्कोल्स और मर्टन को उनकी अंतर्निहित प्रतिभूतियों के जोखिम से स्टॉक विकल्प तलाक देने की विधि की खोज के लिए आर्थिक विज्ञान में 1997 के नोबेल मेमोरियल पुरस्कार से सम्मानित किया गया था। 1995 में फिशर ब्लैक का निधन हो गया, वह पुरस्कार प्राप्त करने के योग्य नहीं थे, लेकिन नोबेल अकादमी द्वारा योगदानकर्ता के रूप में स्वीकार किया गया था।

13.अस्वीकरण(Disclaimer)-

मैं एक गणितीय अर्थशास्त्री नहीं हूं, न ही इसका कोई हिस्सा या मेरे द्वारा प्रकाशित किसी भी लेख का अर्थ वित्तीय सलाह के रूप में है। विकल्प ट्रेडिंग के बारे में अधिक पढ़ने में रुचि रखने वालों के लिए, मैं विशेष रूप से माइकल लुईस द्वारा विशेष रूप से अब प्रसिद्ध पुस्तक "द बिग शॉर्ट" की सिफारिश करता हूं और शायद "इवेंट-संचालित निवेश, विभक्ति अंक, और कैसे मैंने दो में 32x अपना पैसा कमाया सप्ताह "।