Right Circular Cylinder

(1.)लम्ब्वृत्तीय बेलन(Right circular cylinder) :-

लम्ब्वृत्तीय बेलन वह ठोस आकृति है जिसमें एक पृष्ठ और सर्वांगसम वृत्तीय अनुप्रस्थ काट हो तथा बेलन का अक्ष वृत्तीय अनुप्रस्थ काट पर लम्बवत हो।बेलन का अक्ष वृत्तीय अनुप्रस्थ काटों के केंद्रों को मिलाने वाली रेखा होती है।अक्ष के समांतर और पार्श्व पृष्ठ पर स्थित रेखा जनक कहलाती है।चित्र में रेखाएंAB,CD जनक हैं।बेलन के नीचे के वृत्तीय सिरे को आधार,रेखाखंडAB को ऊँचाई तथा वृत्तीय सिरे की त्रिज्याOA कहते हैं।ठोस बेलन के दोनो सिरे बंद होते हैं।

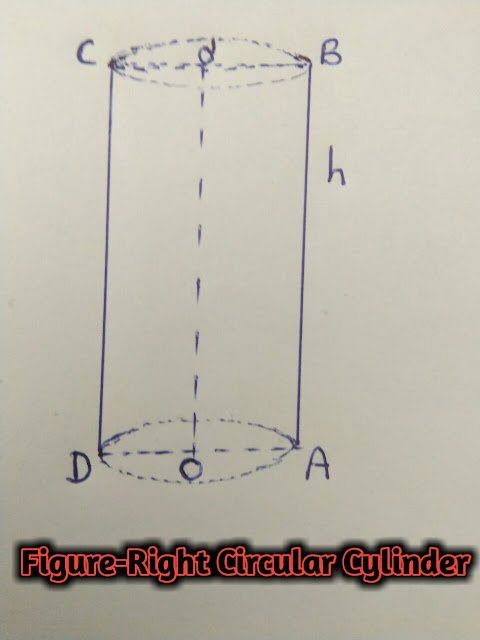Figure-Right Circular Cylinder

अत: हम कह सकते हैं जब किसी आयत OABO^’ की भुजाOO^’ को अक्ष मानकर चारों ओर परिक्रमण कराते हैं,तो एक ठोस बेलन प्राप्त होता है जिसकी ऊँचाईAB तथा त्रिज्याOA के बराबर होती है।यदि बेलन की त्रिज्याr और ऊँचाई hहो,तो बेलन के (i)प्रत्येक सिरे या आधार का क्षेत्रफल =𝜋r²

(ii)बेलन के वक्र पृष्ठ का क्षेत्रफल=आयतOABO^’ का क्षेत्रफल

बेलन के वक्र पृष्ठ का क्षेत्रफल=2𝜋r x h=2𝜋rhवर्गइकाई(iii)अत:बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल=2𝜋rh+2𝜋r²=2𝜋r(h+r)

(iV)बेलन का आयतन=आधार का क्षेत्रफल  xऊँचाई=𝜋r²xh=𝜋r²hघन इकाई

(2.)खोखला बेलन(Hollow Cylinder):-

खोखला बेलन वह आकृति है जो कि दो बेलनों से मिलकर बनती हो।जिनकी ऊँचाई समान और त्रिज्या असमान हों।खोखले बेलन के दोंनों सिरे खुले होते हैं।

Figure-Hollow Cylinder

यदिr₁ औरr₂ खोख्ले बेलन की बाह्य और अंत: त्रिज्या तथा ऊँचाईh हो,तो

(i)प्रत्येक सिरे का क्षेत्रफल=𝜋(r₁²-r₂²)

(ii)वक्र पृष्ठ का क्षेत्रफल=बाह्य पृष्ठ का क्षेत्रफल+अंत: पृष्ठ का क्षेत्रफल=2𝜋r₁h+2𝜋r₂h

वक्र पृष्ठ का क्षेत्रफल=2𝜋h(r₁+r₂)

(iii)अत: खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल=वक्र पृष्ठ का क्षेत्रफल+2(एक सिरे का क्षेत्रफल)=2𝜋(r₁+r₂)h+2𝜋(r₁²-r₂²)=2𝜋(r₁+r₂)+ 2𝜋(r₁+r₂)(r₁-r₂)

खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल=2𝜋(r₁+r₂)(h+r₁-r₂)

(iv)खोखले बेलन का आयतन=बाह्य बेलन का आयतन-अन्त: बेलन का आयतन

 =𝜋r₁²-r₂²𝜋

खोखले बेलन का आयतन=𝜋(r₁²-r₂²)

(3.) Example:-

प्रश्न:-दो लम्बवृत्तीय बेलनों की त्रिज्याओं का अनुपात 2:3 तथा ऊँचाईयों का अनुपात 5:4 है,तो दोनों बेलनों के वक्र पृष्ठीय क्षेत्रफलों तथा आयतनों का अनुपात ज्ञात कीजिए।

उत्तर:-माना पहले बेलन की त्रिज्याr₁=2x     दूसरे बेलन की त्रिज्याr₂=3x

पहले बेलन की ऊँचाईh₁=5y        दूसरे बेलन की त्रिज्याh₂=4y

पहले बेलन का वक्र पृष्ठ का क्षेत्रफलS₁ =2_𝜋 r₁h₁ =2𝜋 (2x)(5y)=20𝜋xy

दूसरे बेलन का वक्र पृष्ठ का क्षेत्रफलS₂ =2𝜋 r₂ h₂=2 (3x)(4y)=24𝜋xy

दोनों बेलनों के वक्र पृष्ठों में अनुपात S₁:S₂= 20𝜋x y:24 𝜋xy=5:6

पहले बेलन का आयतनV₁= 𝜋r₁²h=𝜋(2x)(2x)(5y)=20𝜋 xy

दूसरे बेलन का आयतन  V 2=𝜋 r₂²h=𝜋(3x)(3x)(4y)=36𝜋 xy

दोनों बेलनों के आयतनों में अनुपात V₁:V₂=20 𝜋 x y: 36 𝜋x y=5:9