Differential Equations — Basics

1.विभेदक समीकरण - मूल बातें(Differential Equations — Basics)-

Differential Equations — Basics

आदेश अवलोकन और मानक संकेतन
विभेदक समीकरणों (DFQs) की सुंदर शाखा में अंतर समीकरणों के कई, कई ज्ञात प्रकार मौजूद हैं। वास्तव में, DFQ के बारे में किसी की समझ को रैंप अप करने का सबसे अच्छा तरीका पहले बुनियादी वर्गीकरण प्रणाली से निपटना है। क्यूं कर? क्योंकि आप कभी भी पूरी तरह से विदेशी DFQ में नहीं चलेंगे। अधिकांश DFQs पहले से ही हल किए गए हैं, इसलिए यह अत्यधिक संभावना है कि एक लागू, सामान्यीकृत समाधान पहले से मौजूद है।
समीकरण के गुणों का वर्णन करने के अलावा, अंतरों को वर्गीकृत करने और पहचानने में वास्तविक मूल्य-जोड़ जंप-ऑफ अंक के लिए एक मानचित्र प्रदान करने से आता है। अंतर समीकरणों को हल करने की चाल मूल तरीकों को बनाने के लिए नहीं है, बल्कि सिद्ध समाधानों को वर्गीकृत और लागू करने के लिए है; कई बार, एक कार्यान्वयन योग्य, सामान्यीकृत समाधान में आने के लिए, एक प्रकार के समीकरण को दूसरे प्रकार के समकक्ष समीकरण में बदलने के लिए चरणों की आवश्यकता हो सकती है।

जबकि सैकड़ों अतिरिक्त श्रेणियां और उपश्रेणियाँ हैं, डीएफक्यू का वर्णन करने के लिए उपयोग की जाने वाली चार सबसे सामान्य गुण हैं:(the four most common properties used for describing DFQs are):
(i)साधारण बनाम आंशिक( Ordinary vs Partial)
(ii)रैखिक बनाम गैर-रैखिक(Linear vs Non-Linear)
(iii)सजातीय बनाम गैर-सजातीय(Homogeneous vs Non-Homogeneous)
(iv)विभेदक आदेश(Differential Order)
हालांकि यह सूची किसी भी तरह से विस्तृत नहीं है, यह एक बेहतरीन कदम है जो आम तौर पर DFQ सेमेस्टर कोर्स के पहले कुछ हफ्तों में समीक्षा की जाती है; इन वर्गीकरण श्रेणियों में से प्रत्येक की शीघ्रता से समीक्षा करके, हम आम DFQ प्रश्नों से निपटने के लिए एक बुनियादी स्टार्टर किट से सुसज्जित होंगे।

2.साधारण बनाम आंशिक(Ordinary vs Partial)-

हाथ में प्रश्न में पाए जाने वाले व्युत्पन्न के प्रकार से जंगली उपजी में पाए जाने वाले डीएफक्यू के लिए पहला, सबसे आम वर्गीकरण; बस, क्या समीकरण में कोई आंशिक व्युत्पन्न है?

यदि नहीं, तो यह एक सामान्य अंतर समीकरण (ODE) है। यदि ऐसा होता है, तो यह आंशिक अंतर समीकरण (PDE) है
ODEs में उस एकल चर के आधार पर अंतर के साथ एक एकल स्वतंत्र चर शामिल होता है। एक सामान्य अंतर समीकरण (या ODE) में चरों का असतत (परिमित) सेट होता है; वे अक्सर एक आयामी डायनेमिक सिस्टम मॉडल करते हैं, जैसे कि समय के साथ एक पेंडुलम का झूलना।

दूसरी ओर PDE, काफी अधिक जटिल होते हैं क्योंकि वे आमतौर पर एक से अधिक स्वतंत्र चर को कई आंशिक अंतरों के साथ शामिल करते हैं जो कि ज्ञात स्वतंत्र चर में से एक पर आधारित हो सकते हैं या नहीं भी हो सकते हैं। एसटीईएम में पीडीई बेहद लोकप्रिय हैं क्योंकि वे प्रकृति में कई तरह की घटनाओं का वर्णन करने के लिए प्रसिद्ध हैं, जैसे कि गर्मी, द्रव प्रवाह, या इलेक्ट्रोडायनामिक्स। यह प्रतीत होता है कि अलग-अलग शारीरिक घटनाएं पीडीई के रूप में औपचारिक रूप से औपचारिक हैं; वे स्टोकेस्टिक आंशिक अंतर समीकरणों में अपना सामान्यीकरण पाते हैं।

एक DFQ समीकरण में व्युत्पन्न के प्रकार की पहचान करने में मदद करने के लिए नीचे कुछ उदाहरण दिए गए हैं:

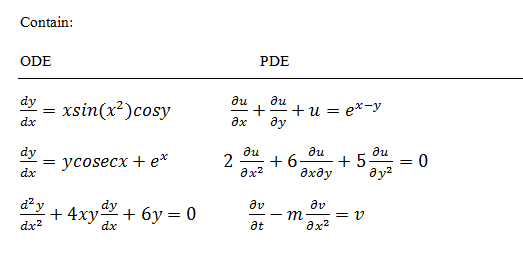Differential Equations — Basics

3.रैखिक बनाम गैर-रैखिक(Linear vs Non-Linear)-

यह दूसरी आम संपत्ति, रैखिकता, द्विआधारी और सीधी है: स्थिरांक और केवल स्थिरांक द्वारा गुणा समीकरण में चर (ओं) और व्युत्पन्न हैं?

यदि ऐसा है, तो यह एक रैखिक DFQ है। अन्यथा, इसे गैर-रैखिक माना जाता है। चर और उनके डेरिवेटिव हमेशा एक साधारण पहली शक्ति के रूप में दिखाई देने चाहिए। उनकी सहज सरलता को देखते हुए, रैखिक समीकरणों को हल करने के सिद्धांत को अच्छी तरह से विकसित किया गया है; यह संभावना है कि आप पहले से ही भौतिकी 101 में उनमें भाग लेंगे।

फिर भी, मुट्ठी भर उदाहरण स्पष्टता के लिए समीक्षा करने के लायक हैं - नीचे DFQ में रैखिकता की पहचान करने की एक तालिका है:

Differential Equations — Basics

4.सजातीय बनाम गैर-सजातीय(Homogeneous vs Non-Homogeneous)-

विभेदक समीकरणों को वर्गीकृत करने का एक तीसरा तरीका, एक DFQ को सजातीय माना जाता है अगर और केवल अगर सभी शब्दों को एक जोड़ या घटाव ऑपरेटर द्वारा अलग किया जाए तो आश्रित चर शामिल है; अन्यथा, यह गैर-सजातीय है। इस संपत्ति की जाँच करने का एक सरल तरीका उन सभी शब्दों को शिफ्ट करना है जिनमें एक समान चिह्न के बाईं ओर निर्भर चर शामिल हैं, अगर दाईं ओर शून्य के अलावा कुछ भी नहीं है, तो यह गैर-सजातीय है।
एक अधिक औपचारिक परिभाषा इस प्रकार है। एक विभेदक समीकरण की परिभाषा को देखें, जो बाएं हाथ की ओर निम्नलिखित चित्र द्वारा दर्शाया गया है:

Differential Equations — Basics

डीएफक्यू को सजातीय माना जाता है यदि आरेख पर दाएं तरफ, जी (एक्स), शून्य के बराबर होता है। यहाँ कुछ उदाहरण दिए गए हैं:

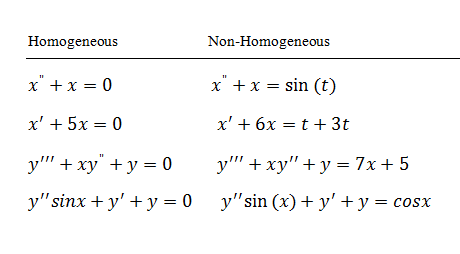Differential Equations — Basics

वास्तविक जीवन के परिदृश्यों में, जी (x) आमतौर पर एक गतिशील, भौतिक मॉडल में एक मजबूर शब्द से मेल खाती है। उदाहरण के लिए, एक मोटराइज्ड पेंडुलम में, यह मोटर होगी जो पेंडुलम को चला रही है और इसलिए जी (x) का नेतृत्व करेगी! = 0।

5.पहला ऑर्डर, दूसरा ऑर्डर(First Order,Second Order)

मूल वर्गीकरणों में से अंतिम, यह निश्चित रूप से एक संपत्ति है जिसे आपने गणित की पूर्वापेक्षा शाखाओं में पहचाना है: एक विभेदक समीकरण का क्रम। उच्चतम एनटी-डिग्री के क्रम का वर्णन करने के विपरीत, जैसा कि बहुपद में होता है, अंतर के लिए, फ़ंक्शन का क्रम समीकरण में उच्चतम व्युत्पन्न के बराबर होता है। बुनियादी के रूप में यह हो जाता है:

Differential Equations — Basics

6.अंत में (In closing)-

और हम वहाँ जाते हैं! चार सबसे आम गुण अंतर समीकरणों को पहचानने और वर्गीकृत करने के लिए उपयोग किए जाते हैं। जैसा कि आप अब तक बता सकते हैं, DFQ लेन का रास्ता वनस्पति विज्ञान के समान है; जब आप पहली बार अंतर समीकरणों का अध्ययन करते हैं, तो उनके उचित समूह में DFQ की पहचान और वर्गीकरण के लिए एक आंख विकसित करना व्यावहारिक है। एक बार पहचाने जाने के बाद, यह अत्यधिक संभावना है कि आप Google खोज को सामान्य, लागू समाधान खोजने से दूर रखें।

बेशक, हम एसटीईएम में हर क्षेत्र के पीछे ड्राइविंग शाखा की गहन खोज के लिए चरण निर्धारित करते हैं; समाधान में पूरी तरह से छलांग लगाने के लिए, सरल सेटअपों पर शोध करके शुरू करें, जैसे कि एक सजातीय प्रथम-ऑर्डर ODE!